Индекс детерминации
Индекс детерминации – это квадрат коэффициента корреляции.
Скорректированный индекс детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:
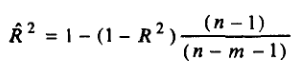, где n – число наблюдений, m – число факторов.
1. Создайте заготовку таблицы для вычислений (см. рисунок).
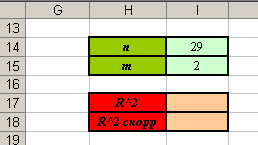
2. В ячейке I17 вычислите квадрат коэффициента корреляции, используя значения находящееся в ячейке I12.
3. В ячейке I18 вычислим скорректированный коэффициент детерминации по имеющейся формуле. Установите курсор в ячейку I18 и введите формулу: =1-(1-I12^2)*(I14-1)/(I14-I15-1).
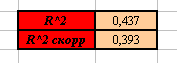
4. Вы должны получить следующие результаты:
Общий вывод:
1. Множественный коэффициент корреляции равен 0.661, следовательно, между результативным и факторным признаком присутствует прямая зависимость средней силы.
2. Из матрицы парных коэффициентов корреляции мы видим, что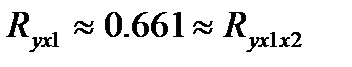 
, при этом между признаками Y и Х2 связь очень слабая: 
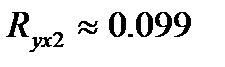. Отсюда можно предположить, что изменение значения признака Х2 практически не влияет на изменении признака Y. Это предположение подтверждает и значение соответствующего среднего коэффициента эластичности: 
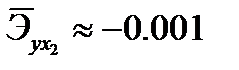. Таким образом, изменения значения факторного признака Х1 на 1% вызовет изменения значения результативного признака Y всего на 0,001%. Следовательно, в основном на изменение значений результативного признака влияет факторный признак Х1: 
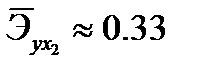, то есть изменение значения факторного признака Х2 на 1% вызовет изменение значения результативного признака на 0,33%.
3. Скорректированный коэффициент детерминации равен 0,393. Это означает, что уравнение регрессии объясняет лишь 39,3% дисперсии результативного признака Y.
Значимость параметров уравнения множественной регрессии
Значимость уравнения множественной регрессии в целом оценивается с помощью F-критерия Фишера:
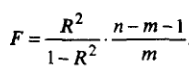, где
n – число наблюдений, m – число факторов (число параметров при неизвестных).
Это фактическое значение сравнивается с табличным значением F-критерия.
Табличное значение критерия определяется при заданном уровне значимости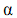 
и степенях свободы 
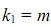и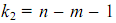 
.
Частный F-критерий оценивает статистическую значимость присутствия каждого из факторов в уравнении. В общем виде для фактора хi частный F-критерий определяется по формуле:
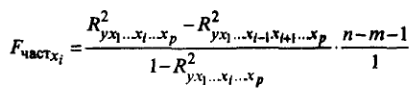
В нашем случае:
; 
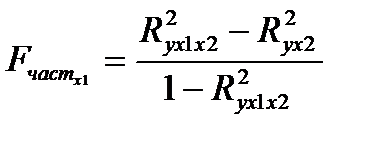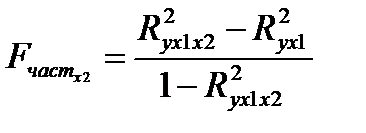
Табличное значение F-критерия для частного критерия определяется при заданном уровне значимости 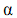и степенях свободы 
.
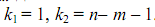1. Сделайте заготовку таблицы для вычислений (см. рисунок).
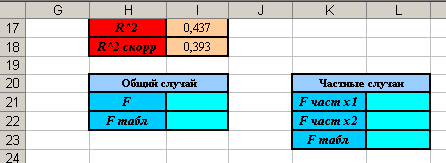
2. Рассчитаем значение F-критерия для всего уравнения в целом. Установите курсор в ячейку I21 и введите формулу: =I17*(I14-I15-1)/((1-I17)*I15).
3. Определим табличное значение F-критерия для всего уравнения регрессии в целом при заданном уровне значимости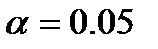 
и степенях свободы 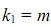и 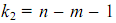. Установите курсор в ячейку I22 и вызовите пункт меню Вставка/Функция… В открывшемся диалоговом окне в категории функций Статистические выберите функцию FРАСПОБР ( ). В открывшемся диалоговом окне задайте следующие параметры: вероятность – 0,05; Степени_свободы1 – I15; Степени_свободы2 - I14-I15-1. Нажмите Ок.
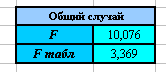
4. Вы должны получить следующие результаты:
5. Вычислим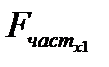 
. Установите курсор в ячейку L21 и введите формулу: =(I17-L5^2)/(1-I17).
6. Вычислим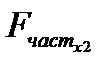 
. Установите курсор в ячейку L22 и введите формулу: =(I17-L4^2)/(1-I17).
7. Получим табличное значение F-критерия для частных случаев. Вставьте в ячейку L23 функцию FРАСПОБР ( ), установив для неё следующие параметры: вероятность – 0,05; Степени_свободы1 – 1; Степени_свободы2 - I14-I15-1.
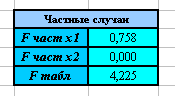
8. Вы должны получить следующие результаты:
Вывод:
1. В общем случае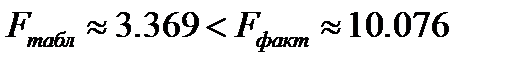 
- следовательно, гипотеза о случайной природе оцениваемых величин отвергается, и с вероятностью 95% можно утверждать, что параметры уравнения множественной регрессии являются значимыми.
2. Для частных случаев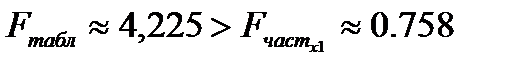 
и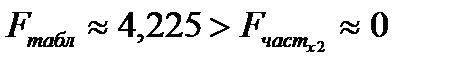 
, то есть присутствие каждого из факторов Х1 и Х2 в уравнении регрессии не значимо.