Индекс множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.
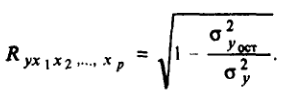, где
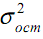- остаточная дисперсия для уравнения 
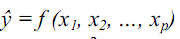, которая вычисляется по формуле:
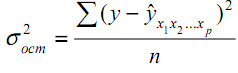
Индекс множественной корреляции для уравнения множественной регрессии в стандартизированном виде определяется по формуле:
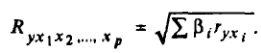
При линейной зависимости коэффициент множественной корреляции можно определить по формуле:
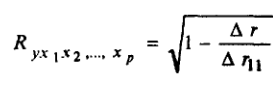, где
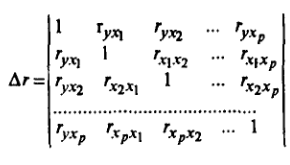- определитель матрицы парных коэффициентов корреляции,
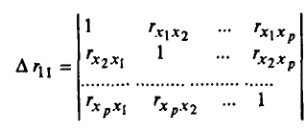- определитель матрицы межфакторной корреляции.
Качество построенной модели оценивают с помощью коэффициента множественной детерминации, который рассчитывается как квадрат индекса множественной корреляции:
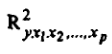
Скорректированный индекс детерминации содержит поправку на число степеней свободы и рассчитывается по формуле:
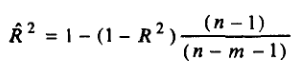, где
n – число наблюдений, m – число факторов.
I способ.
Найдём индекс множественной корреляции по формуле:
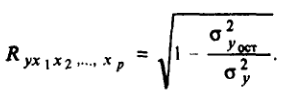
1. В книге MS Excel перейдите на новый лист и скопируйте на него данные с первого листа из диапазона А1:D30 (исходные данные для результативного признака Y и факторных признаков X1 и Х2).
2. Сделайте заготовки таблиц для вычислений (см. рисунок).
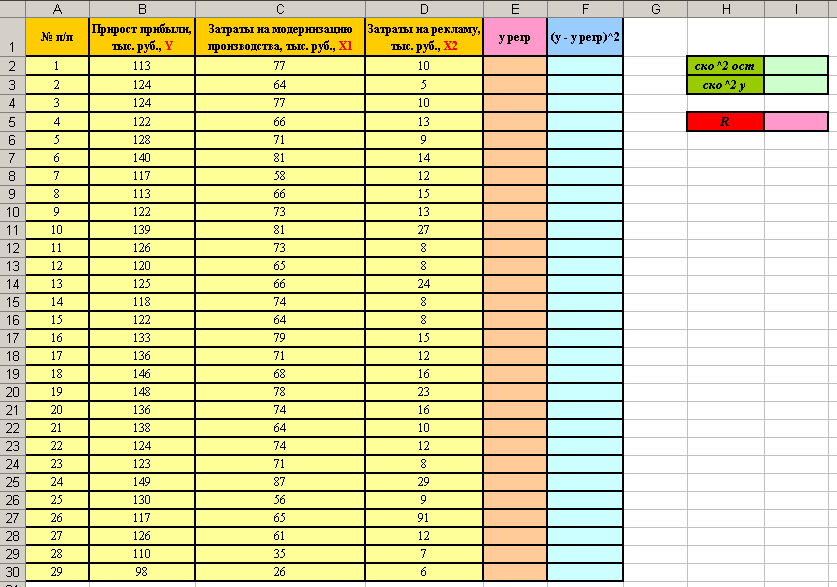
3. Найдём теоретические значения результативного признака Y с помощью полученного уравнения множественной регрессии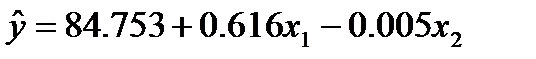 
. В ячейку Е2 введите формулу:
=Лист1!$M$10+Лист1!$M$11*Лист2!C2+Лист1!$M$12*Лист2!D2 (в эту формулу мы подставляем вычисленные значения коэффициентов а, b1 и b2, находящиеся на Листе 1. Скопируйте эту формулу вниз в диапазон ячеек Е3:Е30).
4. В ячейку F2 введите формулу: =(B2-E2)^2. Скопируйте эту формулу вниз в диапазон ячеек F3:F30.
5. В ячейке I2 найдём величину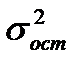 
. Введите в ячейку I2 формулу: =СУММ(F2:F30)/29.
6. В ячейке I3 найдём величину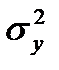 
. Квадрат среднего квадратического отклонения – это дисперсия. Нам требуется найти дисперсию результативного признака Y (данные, находящиеся в диапазоне ячеек В2:В30). Для вычисления дисперсии используем встроенную функцию MS Excel. Введите в ячейку I3 формулу: =ДИСПР(B2:B30).
7. Вычислим индекс множественной корреляции. Введите в ячейку I5 формулу: =КОРЕНЬ(1-I2/I3).
8. Вы должны получить следующие результаты:
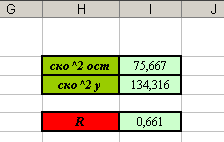
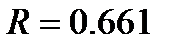
II способ
Найдём индекс множественной корреляции по формуле: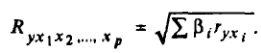
Для этого будем использовать уравнение регрессии в стандартизированном виде:
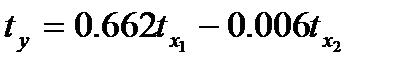
1. Создайте заготовку таблицы для вычислений (см. рисунок).
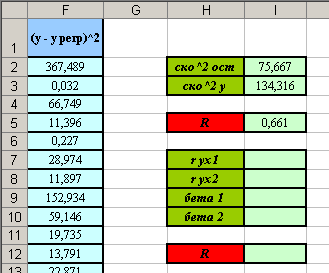
2. С помощью встроенной функции КОРРЕЛ ( ) вычислите в ячейке I7 линейный коэффициент корреляции для результативного признака Y и факторного признака X1.
3. В ячейке I8 вычислите линейный коэффициент корреляции для результативного признака Y и факторного признака Х2.