Линейное уравнение множественной регрессии

Дата: 2025-06-02; Просмотры: 14
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

в стандартизированном виде

 

 

Линейное уравнение множественной регрессии в стандартизированном виде записывается следующим образом:

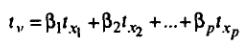
Здесь:

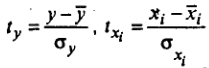- стандартизированные переменные, для которых среднее значение равно нулю ( 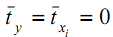), а средние квадратическое отклонение равно единице ( ).

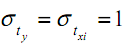Параметры линейного уравнения множественной регрессии в стандартизированном виде можно найти из системы уравнений:

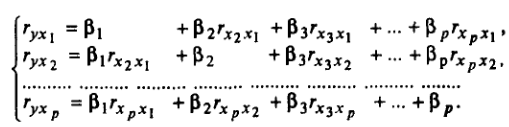
Мы воспользуемся тем, что между коэффициентами множественной регрессии 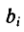и стандартизированными коэффициентами регрессии 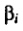существует связь, которая описывается равенством:

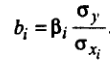
Отсюда стандартизированные коэффициенты регрессии можно найти по формуле:

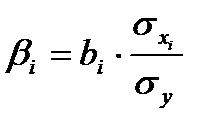
  1. Создайте заготовки таблиц для вычислений (см. рисунок).

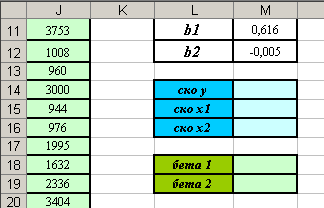
  1. В ячейке М14 вычислите среднее квадратическое отклонение результативного признака y (диапазон ячеек В2:В30), используя функцию СТАНДОТКЛОН ( ).
  2. В ячейке M15 вычислите среднее квадратическое отклонение факторного признака х1 (диапазон ячеек С2:С30).
  3. В ячейке М16 вычислите среднее квадратическое отклонение факторного признака х2 (диапазон ячеек D2:D30).
  4. В ячейку М18 введите формулу: =M11*M15/M14 (находим стандартизированный коэффициент регрессии ).
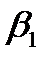  5. В ячейку М19 введите формулу: =M12*M16/M14 (находим ).
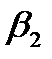  6. Вы должны получить следующие результаты:

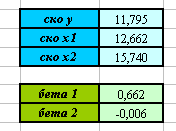
Вывод. Уравнение линейной множественной регрессии в стандартизированном виде для изучаемых данных запишется следующим образом:

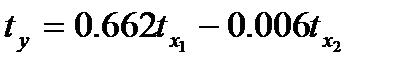
При этом: 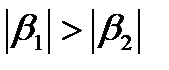, то есть на результативный признак Y большее влияние оказывает фактор Х1, при чём это влияние гораздо сильнее, чем влияние фактора Х2.

 

Средние коэффициенты эластичности

Средние коэффициенты эластичности для линейного уравнения множественной регрессии рассчитываются по формуле:

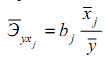
Они показывают, на сколько процентов в среднем по совокупности изменится результат у от своей величины при изменении фактора 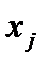на 1% от своего значения при неизменных значениях других факторов.

  1. Сделайте заготовку таблицы для вычислений (см. рисунок).

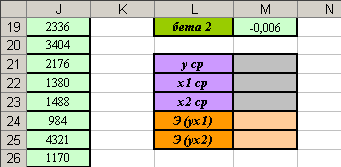
  1. С помощью встроенной функции найдите в ячейке М21 среднее значение результативного признака Y (диапазон ячеек В2:В30).
  2. В ячейке М22 найдите среднее значение факторного признака Х1 (диапазон ячеек С2:С30).
  3. В ячейке М23 найдите среднее значение факторного признака Х2 (диапазон ячеек D2:D30).
  4. В ячейку М24 введите формулу: =M11*M22/M21 (находим коэффициент эластичности 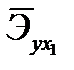по формуле).
  5. В ячейку М25 введите формулу: =M12*M23/M21 (находим ).
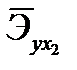  6. Вы должны получить следующие результаты:

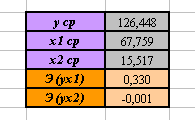
Вывод:

1. С изменением затрат на модернизацию производства (фактор Х1) на 1% прирост прибыли изменится на 0,33% при условии, что затраты на рекламу (фактор Х2) останутся на прежнем уровне.

2. С изменением затрат на рекламу (фактор Х2) на 1% прирост прибыли изменится всего на 0,001% при условии, что затраты на модернизацию производства (фактор Х1) останутся на прежнем уровне.

 

Показатели тесноты связи