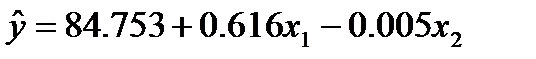Результативный и факторные признаки

Дата: 2025-06-02; Просмотры: 17
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Очевидно, что в данном случае результативным признаком является прирост прибыли, остальные признаки являются факторными.

Введём обозначения:

Y – прирост прибыли, тыс. руб. (результативный признак);

Х1 – затраты на модернизацию производства, тыс. руб. (факторный признак);

Х2 – затраты на рекламу, тыс. руб. (факторный признак);

Х3 – затраты на премирование работников, тыс. руб. (факторный признак).

 

Коллинеарность и мультиколлинеарность

  1. Создайте новую книгу MS Excel;
  2. На первом листе создайте таблицу с исходными данными (см. рисунок).

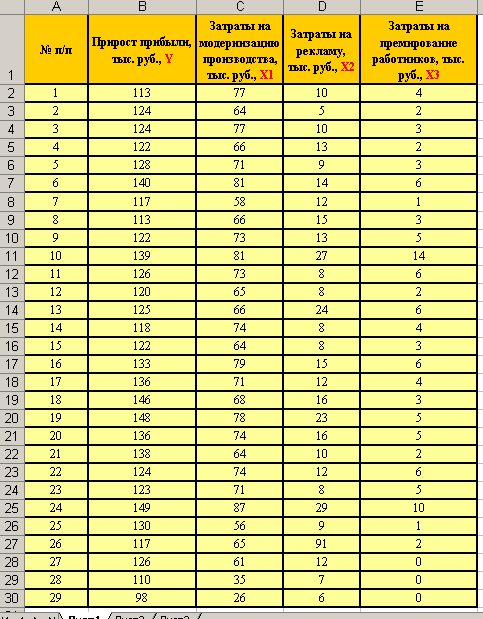
  1. Построим матрицу парных коэффициентов корреляции между факторами. Для построения матрицы парных коэффициентов используем специальные возможности MS Excel.
    1. Вызовите пункт меню Сервис/Анализ данных…
    2. В открывшемся диалоговом окне выберите пункт Корреляция, нажмите ОК.
    3. В новом диалоговом окне задайте следующие параметры: входной интервал – В2:Е30, группирование – по столбцам, выходной интервал – А35. Нажмите ОК.
    4. Вы должны получить следующие результаты:

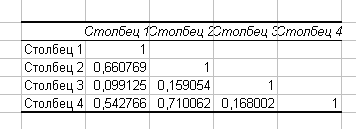
    1. Оформите эту таблицу (см. рисунок).

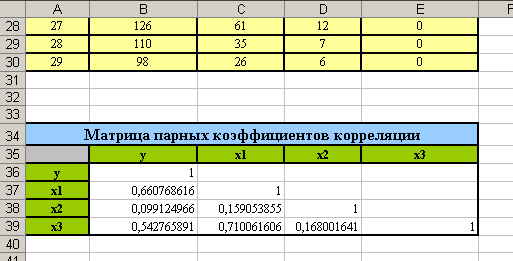
    1. Из полученной матрицы мы видим, что между признаками х1 и х3 существует достаточно сильная корреляционная зависимость: 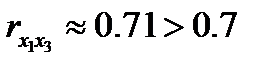. Таким образом факторы х1 и х3 дублируют друг друга. Если бы мы вычислили определитель этой матрицы, то получили бы результат 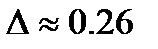, этот результат достаточно близок к нулю, следовательно, присутствует мультиколлинеарность факторов. Нужно решить, какой из факторов (х1 или х3) следует исключить из модели. Для этого нужно оценить тесноту связи обоих факторов с фактором х2, который в любом случае включается в модель: 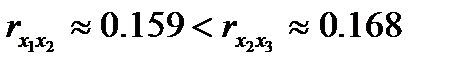. Удаляем тот фактор, для которого связь с фактором х2 теснее. Это фактор х3. Кроме того, по имеющимся данным можно сделать вывод о том, что вряд ли прирост прибыли сильно зависит от затрат на премирование работников: суммы этих затрат для рассматриваемых предприятий невелики или вообще равны нулю.

Вывод: исключим из модели признак х3.

Уравнение множественной регрессии линейного вида

В нашем случае имеется два фактора: х1 и х2. Следовательно, нужно получить уравнение множественной регрессии вида:

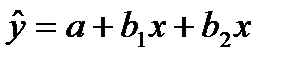
В общем случае для р факторов параметры уравнения линейной множественной регрессии получают из системы уравнений:

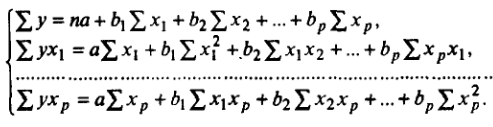
Запишем эту систему для двух факторов:

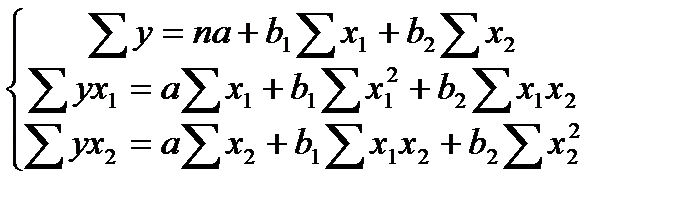
п – это количество наблюдений, в нашем случае их 29.

  1. Вычислим нужные параметры для системы уравнений. Создайте заготовку таблицы для вычислений (см. рисунок).

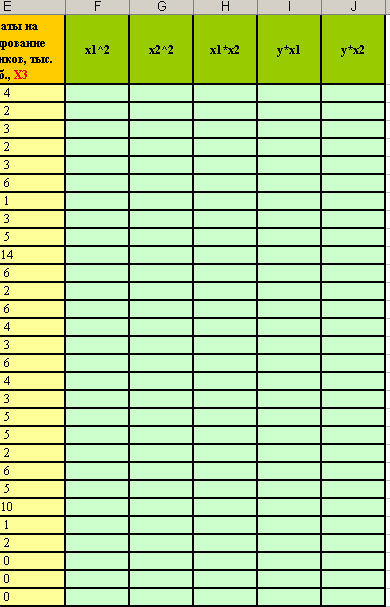
    1. В столбце F с помощью формулы вычислите квадраты чисел, находящихся в столбце С (квадраты значений факторного признака х1).
    2. В столбце G с помощью формулы вычислите квадраты чисел, находящихся в столбце D (квадраты значений факторного признака х2).
    3. В столбце Н вычислите с помощью формулы произведения значений из столбцов C и D (произведения значений факторных признаков х1 и х2).
    4. В столбце I вычислите с помощью формулы произведения значений из столбцов В и С (произведения значений результативного признака y и факторного признака х1).
    5. В столбце J вычислите с помощью формулы произведения значений из столбцов В и D (произведения значений результативного признака y и факторного признака х2).
    6. Вы должны получить следующие результаты:

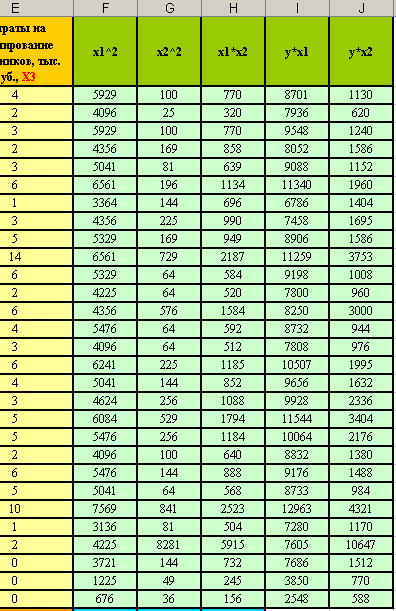
    1. Подсчитайте сумму значений для столбцов B, C, D, E, F, G, Н, I и J в строке 31. Вы должны получить следующие результаты:

    1. Теперь можно составить систему уравнений:

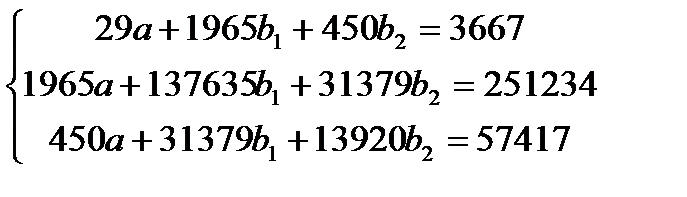
  1. Решим полученную систему уравнений матричным способом. Решение находим по формуле: 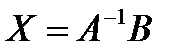. Здесь: А – матрица коэффициентов при переменных, В – вектор-столбец свободных коэффициентов, Х – вектор-столбец неизвестных.
    1. Сделайте заготовки таблиц для вычислений (см. рисунок).

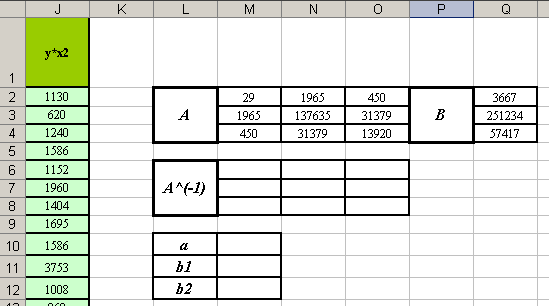
    1. В диапазоне ячеек М6:О9 получите матрицу 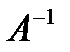(матрицу, обратную матрице коэффициентов при неизвестных А). Для этого используйте функцию МОБР ( ). Не забывайте при использовании этой функции нажимать комбинацию клавиш Ctrl, Shift и Enter.
    2. В диапазоне ячеек М10:М12 получите произведение матриц 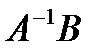с помощью функции МУМНОЖ ( ). Не забывайте при использовании этой функции нажимать комбинацию клавиш Ctrl, Shift и Enter.
    3. Вы должны получить следующие результаты:

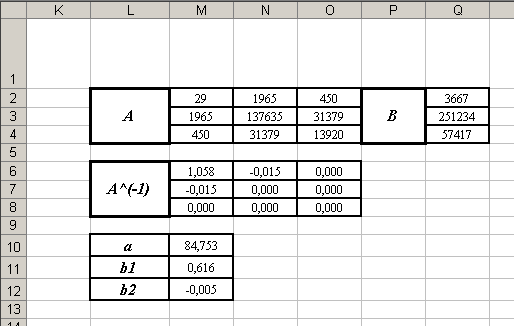
Вывод. Уравнение множественной регрессии линейного вида для изучаемых данных имеет вид: