Множественная регрессия.

Дата: 2025-06-02; Просмотры: 11
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

Гетероскедастичность и гомоскедастичность остатков.

Цель работы

Получение навыков построения уравнения множественной регрессии и проведения анализа на его основе .

Математический аппарат модели множественной линейной регрессии.

Задача многомерного регрессионного анализа состоит в построении модели, позволяющей по значениям независимых переменных получать оценки значений зависимой переменной.

Переменные, участвующие при построении модели, можно разделить на следующие типы.

Результирующая (зависимая, эндогенная) переменная Y.

Она характеризует результат или эффективность функциониро­вания экономической системы. Значения ее формируются в процессе и внутри функционирования этой системы под воздействием ряда других переменных и факторов, часть из которых поддается регистрации, управ­лению и планированию. В регрессион­ном анализе результирующая переменная играет роль функции, значение которой определяется значениями объясняющих переменных, выполняю­щих роль аргументов. По своей природе результирующая переменная все­гда случайна (стохастична).

Объясняющие (независимые, экзогенные) переменные X - это переменные, которые поддаются регистрации и описывают условия функционирования реальной экономической системы. Они в зна­чительной мере определяют значения результирующих переменных. Обычно часть из них поддается регулированию и управлению. Еще их называют факторными признаками. В регрессионном анализе это аргументы ре­зультирующей функции Y. По своей природе они могут быть как случай­ными, так и неслучайными.

В то время как зависимая переменная должна быть непрерывной (за исключением логистической регрессии), независимые переменные могут быть как прерывными, так и категориальными, такими как «пол» или «тип применяемого препарата». Если все независимые переменные являются категориальными (или большинство из них являются категориальными), то в этом случае лучше использовать дисперсионный анализ.

Функция 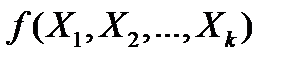, оп исывающая зависимость показателя от параметров, называется уравнением (функцией) регрессии[1]. Уравнение регрессии показывает ожидаемое значение зависимой переменной 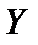при определенных значениях зависимых переменных .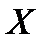