Рис. 1.13 Графическое представление результата сложения трех периодических сигналов: а) временные диаграммы; б) амплитудно-частотный спектр
Причем, частота (F = 1/Т) сигналов u 2 и u 3 является кратной F 1, т.е. F 2 =2F 1 и F 3 =3F 1 . Справа от временных диаграмм (рис. 1.13,б), сигналы представлены в виде амплитудно-частотного спектра. На этих диаграммах, ось абсцисс образует шкалу частот f = nF 1, где n - целое число, а на оси ординат откладываются отрезки, длина которых пропорциональна амплитудным значениям Unm сигналов (без учета начальных фаз гармоник).
Как видим (рис. 1.13,а), форма суммарного сложного сигнала u Ʃ, повторяется через временной промежуток Т. Следовательно, этот сигнал является периодическим, период колебания которого, равен периоду колебания сигнала u 1, т.е. Т = Т1.
Таким образом, если результатом сложения нескольких гармонических сигналов, является периодический сложный сигнал, то, очевидно, и любой сложный периодический сигнал можно разложить на простейшие гармонические составляющие.
Так в соответствии с [11], любой сложный периодический сигнал можно представить в виде совокупности простейших гармонических сигналов, значения амплитуд (Unm), частот (ω n) и начальных фаз (φ n) которых, можно найти посредством разложения в ряд Фурье:
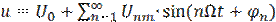, (1.2)
где n = 1,2,3… - целое число, а Ω = 2π F, F =1/Т.
Примечание. В дальнейшем, частоту высокочастотного колебания будем обозначать буквой f , а низкочастотного – F .
Гармонические сигналы, частота которых F 1 = F , F 2 = 2F , F 3 = 3F и т.д. именуются соответственно: первая, вторая, третья гармоники.
Таким образом, спектр сигнала – это совокупность гармоник (гармонических составляющих) с конкретными значениями частот и амплитуд, образующих в сумме сложный электрический сигнал. Спектр может быть представлен в виде графического изображения, т.е. изображения амплитуд гармоник на оси частот (рис. 1.13, б).
Характерно, что спектр периодических сигналов не сплошной, а линейчатый, т. е. между соседними линиями спектра имеются «просветы» шириной в частоту следования сигнала F = 1/Т.
Более сложный сигнал, например, приведенный на рис. 1.9 (круче изгибы), характеризуется большим количеством составляющих от F н до F в, где F н и F в соответственно нижняя и верхняя составляющие спектра сигнала.
Интервал (диапазон) частот F в - F н = Δ F называется шириной спектра сигнала. Ширина спектра сигнала – это интервал (диапазон) частот, в пределах которого сосредоточена основная часть энергии сигнала.
Так, с пектр звукового сигнала (музыка и пение, включающие в себя и спектр речи) имеет общую ширину 20...20 000 Гц и зависит от класса вещания:
1-ый класс – 50...10 000 Гц; высший класс – 30...15 000 Гц и т.д.
Частотный спектр речи лежит в пределах: от 50 Гц до 10 000 Гц. Частота основного тона речи находится в пределах от 50...80 Гц (самый низкий мужской) до 200...250 Гц (самый высокий женский или детский).
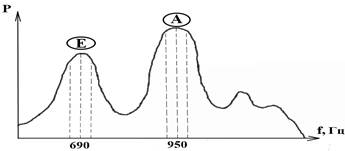
Звуки речи различных людей отличаются количеством формант (спектральных областей резонанса при произношении звуков речи) и их мощностью. Из рис. 1.14 [3] видно, что форманта буквы «А» находится в спектре частот, близких к частоте 950 Гц, а форманта буквы «Е» - к частоте 690 Гц. Установлено экспериментально, что все остальные форманты гласных и согласных звуков, из которых складывается речь, не выходят за пределы спектра 300...3400 Гц.
