Логарифмическая регрессия
Логарифмическая регрессия имеет вид:
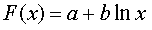
Делаем подстановку:
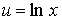
Таким образом, мы перейдём к линейной функции: 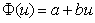
Для нахождения значений параметров а и b нужно прологарифмировать значения аргумента в исходной таблице и найти для новой таблицы приближающую функцию в виде линейной и найденные значения параметров подставить в 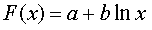
Таким образом, мы будем строить уравнение линейной регрессии для переменных 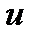 и
и 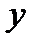 (
( 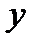 зависит от
зависит от 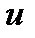 ).
).
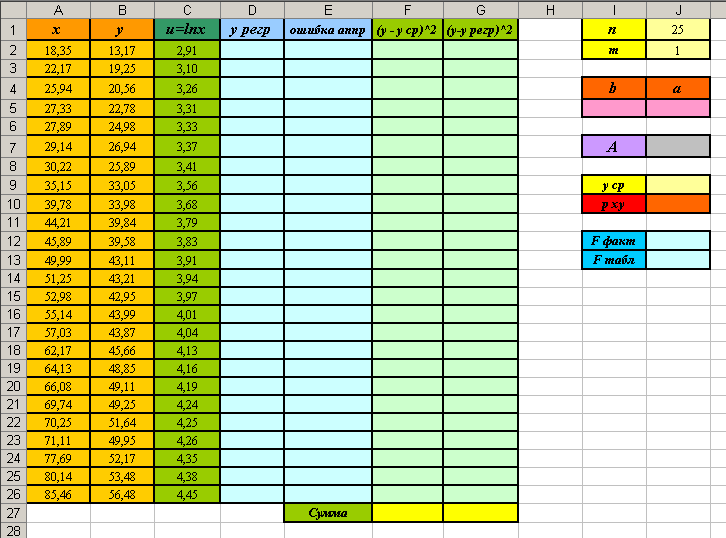
- Вставьте в книгу MS Excel новый лист и создайте на нём заготовки таблиц для вычислений (см. рисунок).
- Прологарифмируем значения аргумента (значения признака Х), то есть получим значения
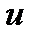 . Установите курсор в ячейку С2 и введите формулу: =LN(A2). Скопируйте эту формулу вниз в диапазон ячеек С3:С26.
. Установите курсор в ячейку С2 и введите формулу: =LN(A2). Скопируйте эту формулу вниз в диапазон ячеек С3:С26. - Найдём параметры а и b уравнения линейной регрессии
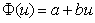 . Получите эти параметры самостоятельно в ячейках I5:J5 с помощью функции ЛИНЕЙН ( ). Вы должны получить следующие результаты:
. Получите эти параметры самостоятельно в ячейках I5:J5 с помощью функции ЛИНЕЙН ( ). Вы должны получить следующие результаты:

Вывод: уравнение логарифмической регрессии имеет вид - 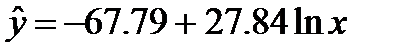
- Построим график логарифмической регрессии и график эмпирической функции в одной системе координат.
- Вычислим теоретические значения прироста прибыли, используя полученное уравнение логарифмической регрессии (то есть будем подставлять имеющиеся значения Х в полученное уравнение регрессии). Установите курсор в ячейку D1 и введите формулу: =$J$5+$I$5*LN(A2). Скопируйте эту формулу в диапазон ячеек D2:D 26.
- Выделите два несмежных диапазона А2:А26 и D2:D26 (для выделения несмежных диапазонов удерживайте нажатой клавишу Ctrl).
- Вызовите пункт меню Вставка/Диаграмма. В открывшемся диалоговом окне выберите тип диаграммы – точечная. Нажмите кнопку Готово. Вы должны получить следующий график:
- Скройте легенду.
- Двойным щелчком на маркерах построенной диаграммы вызовите окно свойств. В этом окне в левой его части установите тип линии – обычная (вместо отсутствует).
- Выделите диаграмму и в пункте меню Диаграмма выберите пункт Добавить данные.
- В открывшемся диалоговом окне задайте диапазон В2:В26. Нажмите ОК.
- Задайте для диаграммы заголовок и подписи осей.
- Найдём среднюю ошибку аппроксимации уравнения линейной регрессии по формуле:
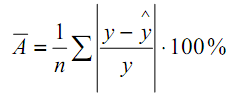
Средняя ошибка аппроксимации должна быть не больше 10% - 12%.
a. Установите курсор в ячейку Е2 и введите формулу: =ABS((B2-D2)/B2). Скопируйте эту формулу вниз в диапазон ячеек Е3:Е26.
b. Установите для ячейки J7 процентный формат и введите в эту ячейку формулу: (вычисляем среднюю ошибку аппроксимации по формуле).
c. Вы должны получить стандартную ошибку аппроксимации 2.90%, это означает, что использование линейной регрессии в данном случае допустимо.
А = 2,9% - использование логарифмической регрессии допустимо
- Вычислим индекс корреляции по формуле:
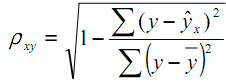
- В ячейке J9 найдите среднее значение результативного признака Y.
- В ячейку F2 введите формулу: =(B2-$J$9)^2. Скопируйте эту формулу вниз в диапазон ячеек F3:F26 (находим величину
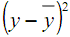 ).
). - В ячейку G2 введите формулу: =(B2-D2)^2. Скопируйте эту формулу вниз в диапазон ячеек G3:G26 (находим величину
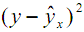 ).
). - Подсчитайте в ячейках F27 и G27 сумму значений из соответствующих столбцов.
- Рассчитаем индекс корреляции по формуле. В ячейку J10 введите формулу: =КОРЕНЬ(1-G27/F27). Вы должны получить индекс корреляции, равный 0,9952 (округлите результат до четырёх знаков после запятой).
Вывод: 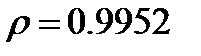 - между признаками присутствует тесная связь.
- между признаками присутствует тесная связь.
- Оценим значимость параметров уравнения линейной регрессии с помощью F-критерия.
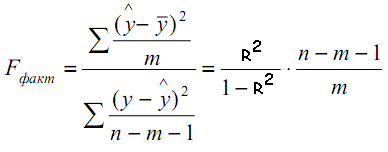
В этой формуле: n = 25 – объём совокупности, m = 1 – число параметров при переменных.
Табличное значение F-критерия определяется для заданного уровня значимости 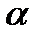 и степенях свободы k1 = m = 1 и k2 = n – m – 1 = 25 – 1 – 1=23.
и степенях свободы k1 = m = 1 и k2 = n – m – 1 = 25 – 1 – 1=23.
- Рассчитаем фактическое значение F-критерия по формуле. Установите курсор в ячейку J12 и введите формулу: =J10*J10*(J1-J2-1)/(J2*(1-J10*J10)).
- Получим табличное значение F-критерия с помощью встроенной функции для уровня значимости
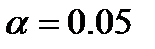 и степеней свободы k1 = 1 и k2= n– m–1 =25–1–1=23. Установите курсор в ячейку J13 и вызовите пункт меню Вставка/Функция. Укажите категорию функций Статистические и выберите функцию FРАСПРОБР ( ). В открывшемся диалоговом окне укажите вероятность 0.05 (это уровень значимости
и степеней свободы k1 = 1 и k2= n– m–1 =25–1–1=23. Установите курсор в ячейку J13 и вызовите пункт меню Вставка/Функция. Укажите категорию функций Статистические и выберите функцию FРАСПРОБР ( ). В открывшемся диалоговом окне укажите вероятность 0.05 (это уровень значимости 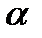 ), Степень_свободы1 – ячейка J2, Степень_свободы2 – J1-J2-1.
), Степень_свободы1 – ячейка J2, Степень_свободы2 – J1-J2-1. - Вы должны получить следующие результаты:
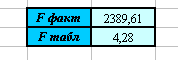
Вывод: 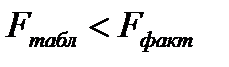 - следовательно, гипотеза о случайной природе оцениваемых величин отвергается, и с вероятностью 95% можно утверждать, что параметры уравнения регрессии и индекс корреляции являются значимыми.
- следовательно, гипотеза о случайной природе оцениваемых величин отвергается, и с вероятностью 95% можно утверждать, что параметры уравнения регрессии и индекс корреляции являются значимыми.
- Спрогнозируем прирост прибыли предприятия, если затраты на модернизацию составят 100 тыс. руб.
- В ячейку А27 введите значение 100.
- Из ячейки D26 скопируйте формулу в ячейку D27. В результаты вы получите искомое ожидаемое значение прироста прибыли. Вы должны получить 60.44 тыс. руб.
Ожидаемый прирост прибыли при затратах на модернизацию производства в 100 тыс. руб. составляет 60.44 тыс. руб.
- Найдём коэффициент эластичности. Он рассчитывается по формуле:
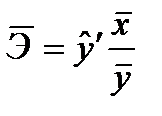
В нашем случае: 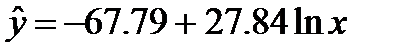 . Отсюда:
. Отсюда: 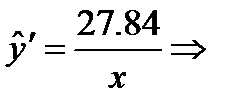
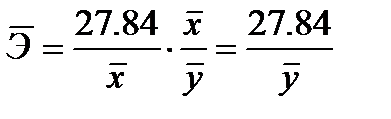 .
.
c. Сделайте заготовку таблицы (см. рисунок).
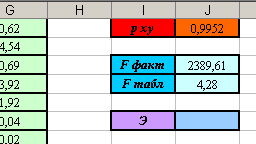
d. Введите в ячейку J15 формулу: =I5/J9. Вы должны получить результат Э = 0,71.
Вывод: при изменении значения признака Х (затрат на модернизацию) на 1% значение признака Y (прирост прибыли) в среднем изменится на 0,71%.
Общие выводы:
- Между затратами на модернизацию производства существует тесная прямая связь, близкая к функциональной.
- В данном случае допустимо использовать линейную, логарифмическую и квадратичную регрессию. Параметры этих видов регрессий и соответствующих им индексов корреляции в данном случае будут значимыми.
- Наиболее удачным в данном случае будет использование логарифмической регрессии – для неё получена минимальная средняя ошибка аппроксимации.
Контрольные вопросы
- Для чего используется корреляционно-регрессионный анализ?
- Как определить вид уравнения регрессии, подходящий для изучаемых данных?
- Что такое средняя ошибка аппроксимации? Какие у неё допустимые пределы?
- Каким образом оценить тесноту связи между величинами?
- Как определить значимость параметров уравнения регрессии и индекса корреляции?
- Каким образом можно спрогнозировать значение результативного признака?
Самостоятельное задание
Для приведённых ниже данных:
- построить поле корреляции;
- выбрать подходящий вид регрессии (не линейной);
- построить уравнение линейной регрессии и уравнение регрессии выбранного вами вида;
- получить среднюю ошибку аппроксимации для каждого уравнения регрессии, сделать вывод о том, как из них в данном случае предпочтительнее;
- вычислить линейный коэффициент корреляции и индекс корреляции;
- оценить значимость параметров уравнений регрессии и показателей тесноты связи;
- для параметров уравнения линейной регрессии и линейного коэффициента корреляции определить доверительные интервалы;
- с помощью обоих видов регрессий спрогнозировать значение результативного признака
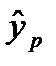 , используя прогнозное значение факторного признака
, используя прогнозное значение факторного признака 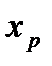 ;
; - в случае линейной регрессии найти доверительный интервал для прогнозного значения результативного признака
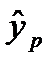 .
.
Данные для самостоятельной работы
K – последняя цифра номера зачетной книжки
| Факторный признак Х | Результативный признак Y |
| 15,98*K | 33,89*(K+1) |
| 16,77*(K+1) | 35,64*(K+1) |
| 19,58*(K-1) | 39,14*(K-1) |
| 20,14*K | 42,15*K |
| 22,59*K | 43,08*(K-1) |
| 25,17*(K+1) | 45,87*(K+1) |
| 29,08*(K+1) | 46,14*K |
| 30,25*K | 49,73*(K-1) |
| 31,44*K | 49,91*(K+1) |
| 37,89*K | 52,08*K |
| 34,99*(K+1) | 52,64*(K+1) |
| 35,15*K | 55,61*(K-1) |
| 40,18*(K+1) | 57,98*K |
| 42,11*K | 59,14*(K-1) |
| 50,09*(K-1) | 63,45*(K-1) |
Лабораторная работа №3








