Линейная регрессия
Линейная регрессия задаётся уравнением:
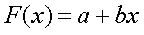
Параметры а и b находятся по формулам:
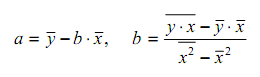
- Создайте на втором листе книги MS Excel таблицы для вычислений (см. рисунок).
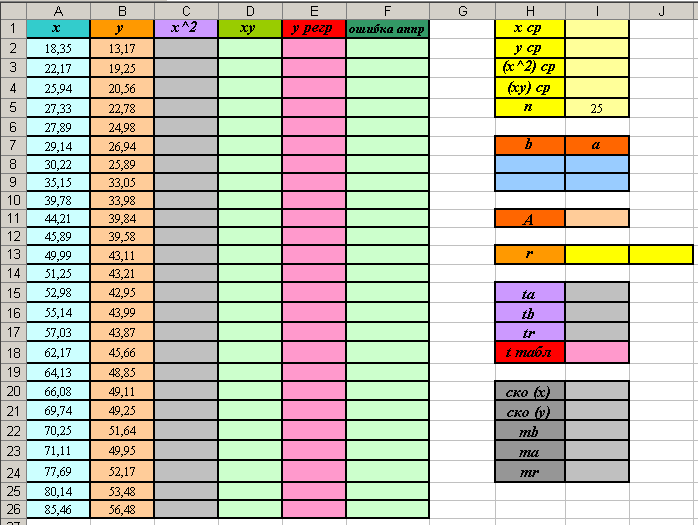
- Установите курсор в ячейку С2 и введите формулу: =А2^2. Скопируйте эту формулу вниз в диапазон ячеек С3:С26 (таким образом мы вычислим квадраты факторного признака Х – затрат на модернизацию производства).
- Установите курсор в ячейку D2 и введите формулу: =A2*B2. Скопируйте эту формулу вниз в диапазон ячеек D3:D26 (для каждой пары Х и У мы вычисляем величину
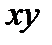 ).
). - В ячейке I1 с помощью встроенной функции вычислите среднее значение для данных из диапазона А2:А26 (находим величину
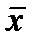 ).
). - В ячейке I2 с помощью встроенной функции вычислите среднее значение для данных из диапазона В2:В26 (находим величину
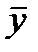 ).
). - В ячейке I3 с помощью встроенной функции вычислите среднее значение для данных из диапазона С2:С26 (находим величину
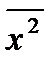 ).
). - В ячейке I4 с помощью встроенной функции вычислите среднее значение для данных из диапазона D2:D26 (находим величину
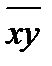 ).
). - Установите курсор в ячейку H8 и введите формулу: =(I4-I2*I1)/(I3-I1*I1) (находим параметр b уравнения линейной регрессии по формуле).
- Установите курсор в ячейку I8 и введите формулу: =I2-H8*I1 (находим параметр а уравнения линейной регрессии по формуле).
- MS Excel позволяет найти параметры уравнения линейной регрессии с помощью специальной формулы:
- Выделите ячейки H9:I9.
- Вызовите пункт меню Вставка/Функция.
- В открывшемся диалоговом окне выберите категорию Статистические, затем в этой категории выберите функцию ЛИНЕЙН, нажмите ОК.
- В открывшемся диалоговом окне в поле Известные значения Y задайте диапазон В2:В26, в поле Известные значения Х задайте диапазон А2:А26. Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив).
- Если все действия выполнены верно, таблица будет иметь вид:
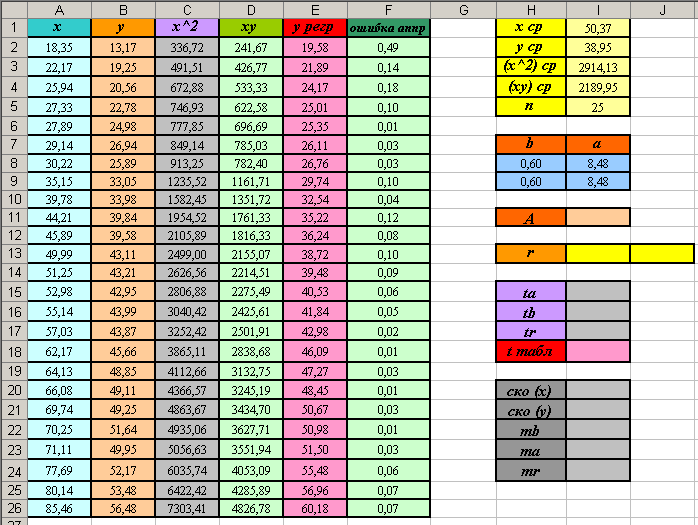
Вывод: уравнение линейной регрессии имеет вид 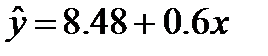
- Постройте график линейной регрессии и график эмпирической функции в одной системе координат.
- Вычислимте теоретические значения прироста прибыли, используя полученное уравнение линейной регрессии (то есть будем подставлять имеющиеся значения Х в полученное уравнение регрессии). Установите курсор в ячейку Е1 и введите формулу: =$H$8+$G$8*A2. Скопируйте эту формулу в диапазон ячеек Е2:Е26.
- Выделите два несмежных диапазона А2:А26 и Е2:Е26 (для выделения несмежных диапазонов удерживайте нажатой клавишу Ctrl).
- Вызовите пункт меню Вставка/Диаграмма. В открывшемся диалоговом окне выберите тип диаграммы – точечная. Нажмите кнопку Готово. Вы должны получить следующий график:
- Скройте легенду.
- Двойным щелчком на маркерах построенной диаграммы вызовите окно свойств. В этом окне в левой его части установите тип линии – обычная (вместо отсутствует).
- Выделите диаграмму и в пункте меню Диаграмма выберите пункт Добавить данные.
- В открывшемся диалоговом окне задайте диапазон В2:В26. Нажмите ОК.
- Задайте для диаграммы заголовок и подписи осей.
- Найдите среднюю ошибку аппроксимации уравнения линейной регрессии по формуле:
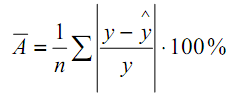
Средняя ошибка аппроксимации должна быть не больше 10% - 12%.
- Установите курсор в ячейку F2 и введите формулу: =ABS((B2-E2)/B2). Скопируйте эту формулу вниз в диапазон ячеек F3:F26.
- Установите для ячейки I11 процентный формат и введите в эту ячейку формулу: =СУММ(F2:F26)/I5 (вычисляем среднюю ошибку аппроксимации по формуле).
- Вы должны получить стандартную ошибку аппроксимации 7,82%, это означает, что использование линейной регрессии в данном случае допустимо.
А = 7,82%
- Оценим тесноту связи с помощью линейного коэффициента корреляции, который вычисляется по формуле:
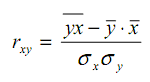
- В ячейке I20 рассчитайте среднее квадратическое отклонение для факторного признака Х, используя встроенную функцию СТАНДОТКЛОН ( ) (диапазон ячеек А2:А26).
- Аналогичным образом в ячейке I21 рассчитайте среднее квадратическое отклонение для результативного признака Y.
- Вычислим коэффициент корреляции по формуле. Установите курсор в ячейку I13 и введите формулу: =(I4-I2*I1)/(I20*I21).
- MS Excel содержит встроенную функцию, позволяющую вычислить линейный коэффициент корреляции. Установите курсор в ячейку J13 и вызовите пункт меню Вставка/Функция. В категории функций статистические выберите функцию КОРРЕЛ ( ). В открывшемся диалоговом окне в поле Массив 1 задайте диапазон А2:А26 (значения признака Х), а в поле Массив 2 – диапазон В2:В26 (значения признака Y). Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив). Внимание! Результаты, полученные по формуле и с помощью функции, могут различаться! Это связано с накопившейся погрешностью вычислений.
r>0.9, следовательно, между величинами присутствует сильная прямая взаимосвязь.
- Оценим значимость параметров уравнения регрессии, используя критерий Стьюдента. Нам нужно будет вычислить фактические значения t-критерия по формулам:
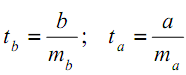
В этих формулах:
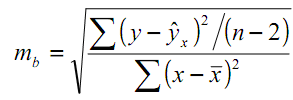 ,
, 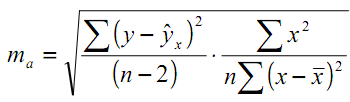
- стандартные ошибки.
- Создайте заготовку таблицы для вычислений на том же рабочем листе (см. рисунок).
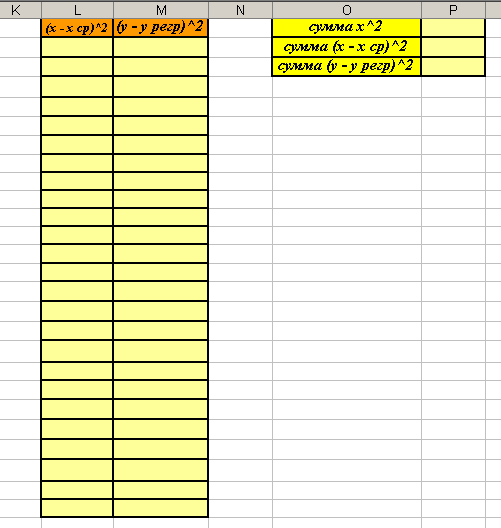
- Установите курсор в ячейку L2 и введите формулу: =(A2-$I$1)^2. Скопируйте эту формулу вниз в диапазон ячеек L3:L26 (для каждого значения признака Х мы находим величину
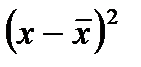 ).
). - Установите курсор в ячейку М2 и введите формулу: =(B2-E2)^2. Скопируйте эту формулу вниз в диапазон ячеек М3:М26 (находим величину
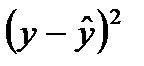 ).
). - В ячейке Р1 с помощью функции вычислите сумму чисел из диапазона ячеек С2:С26 (сумма квадратов аргумента Х, она используется в формуле).
- В ячейке Р2 с помощью функции вычислите сумму чисел из диапазона ячеек L2:L26.
- В ячейке Р3 с помощью функции вычислите сумму чисел из диапазона ячеек М2:М26.
- Установите курсор в ячейку I22 и введите формулу: =КОРЕНЬ(P3/((I5-2)*P2)) (находим величину
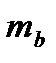 ).
). - Установите курсор в ячейку I23 и введите формулу: =КОРЕНЬ((P3*P1)/(I5*(I5-2)*P2)) (находим величину
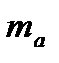 ).
). - Установите курсор в ячейку I15 и введите формулу: =I8/I23 (находим величину
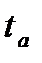 ).
). - Установите курсор в ячейку I16 и введите формулу: =H8/I22 (находим величину
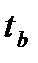 ).
). - Найдём табличное значение t-критерия. В нашем случае число степеней свободы
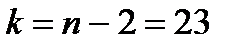 , уровень значимости
, уровень значимости 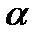 возьмём равным 0,05. Установите курсор в ячейку I18 и введите формулу: =СТЬЮДРАСПОБР(0,05;I5-2).
возьмём равным 0,05. Установите курсор в ячейку I18 и введите формулу: =СТЬЮДРАСПОБР(0,05;I5-2). - Вы должны получить следующие результаты:
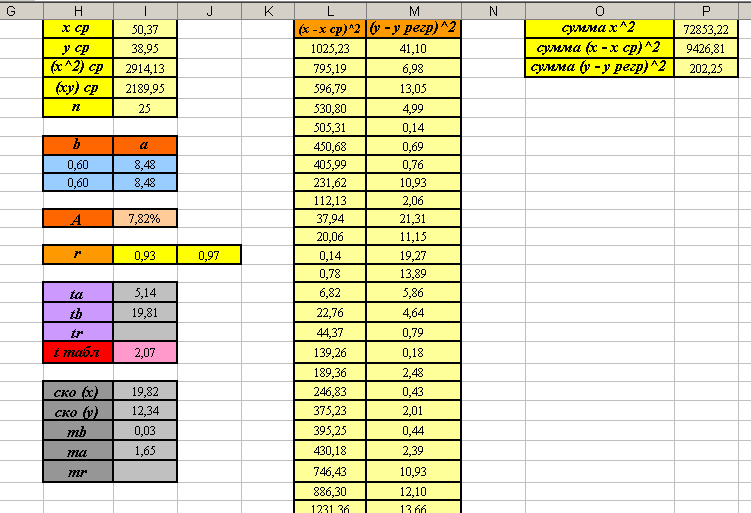
Выводы: 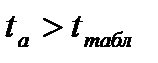 и
и 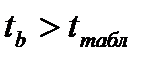 - с вероятностью 95% гипотеза о случайной природе формирования параметров линейной регрессии отвергается, параметры уравнения а и b признаются значимыми.
- с вероятностью 95% гипотеза о случайной природе формирования параметров линейной регрессии отвергается, параметры уравнения а и b признаются значимыми.
- Оценим значимость линейного коэффициента корреляции. Для этого используем следующие формулы:
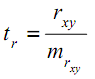
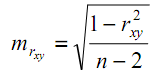 - стандартная ошибка.
- стандартная ошибка.
- Установите курсор в ячейку I24 и введите формулу: =КОРЕНЬ((1-I13^2)/(I5-2)) (находим стандартную ошибку по формуле).
- Установите курсор в ячейку I17 и введите формулу: =I13/I24 (находим фактическое значение t-критерия).
- Вы должны получить следующие результаты:
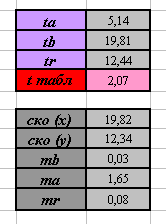
Вывод: 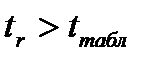 - с вероятностью 95% можно утверждать, что коэффициент линейной корреляции не случайно отличается от нуля, поэтому он признаётся значимым.
- с вероятностью 95% можно утверждать, что коэффициент линейной корреляции не случайно отличается от нуля, поэтому он признаётся значимым.
- Построим доверительные интервалы для параметров уравнения линейной регрессии. Для этого используем следующие формулы:
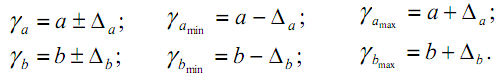
В этих формулах:
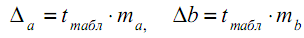 - предельные ошибки показателей.
- предельные ошибки показателей.
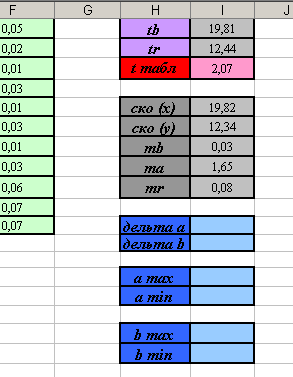
- Создайте на листе заготовку таблицы для вычислений (см. рисунок).
- Вычислим
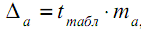 . Установите курсор в ячейку I26 и введите формулу: =I18*I23.
. Установите курсор в ячейку I26 и введите формулу: =I18*I23. - Вычислим
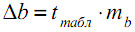 . Установите курсор в ячейку I27 и введите формулу: =I18*I22.
. Установите курсор в ячейку I27 и введите формулу: =I18*I22. - Самостоятельно рассчитайте границы доверительных интервалов, используя формулы приведённые выше. Вы должны получить следующие результаты:
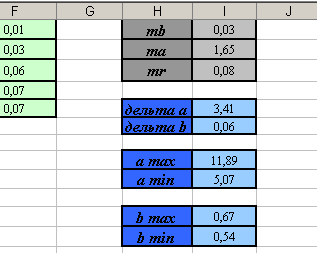
Вывод: с вероятностью 95% можно утверждать, что параметр а уравнения линейной регрессии принадлежит промежутку от 5,07 до 11,89, а параметр b принадлежит промежутку от 0,54 до 0,67.
- Построим доверительный интервал для линейного коэффициента корреляции. Для этого будем использовать Z-распределение Фишера:
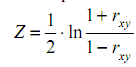
Нам потребуется получить интервальные оценки по формуле:
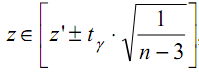
То есть вначале мы найдём доверительный интервал для величины z.
В этой формуле:
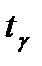 - значение случайной величины, подчиняющейся стандартному нормальному распределению, соответствующему вероятности
- значение случайной величины, подчиняющейся стандартному нормальному распределению, соответствующему вероятности 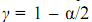 (альфа – уровень значимости).
(альфа – уровень значимости).
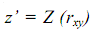 - значение Z-распределения Фишера, соответствующее полученному значению линейного коэффициента парной корреляции (нам нужно будет подставить значение коэффициента корреляции в формулу для z).
- значение Z-распределения Фишера, соответствующее полученному значению линейного коэффициента парной корреляции (нам нужно будет подставить значение коэффициента корреляции в формулу для z).
Граничные значения доверительного интервала для коэффициента корреляции получают из границ доверительного интервала для z с помощью функции, обратной Z-распределению Фишера.
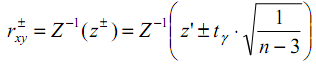
Обратное значение для z будет определяться по формуле:
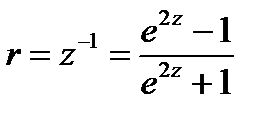
То есть, нам нужно будет подставить в эту формулу значения границ доверительного интервала для z и в результате мы получим доверительные интервалы для r.
- Создайте заготовку таблицы для вычислений (см. рисунок).

- Найдите значение
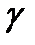 . В ячейку В30 введите формулу: =1-0,05/2 (0,05 – это уровень значимости
. В ячейку В30 введите формулу: =1-0,05/2 (0,05 – это уровень значимости 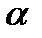 ).
). - Найдите значение величины
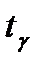 . Мы имеем дело с величиной, имеющей стандартное нормальное распределение. Таким образом, мы ищем значение величины, имеющей стандартное нормальное распределение, при уровне значимости
. Мы имеем дело с величиной, имеющей стандартное нормальное распределение. Таким образом, мы ищем значение величины, имеющей стандартное нормальное распределение, при уровне значимости 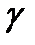 . Используем встроенную функцию. В ячейку В31 введите формулу: =НОРМСТОБР(B30).
. Используем встроенную функцию. В ячейку В31 введите формулу: =НОРМСТОБР(B30). - В ячейку В32 введите формулу: =0,5*LN((1+I13)/(1-I13)) (находим значение
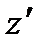 по формуле
по формуле 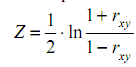 , подставляя в неё найденное значение коэффициента корреляции).
, подставляя в неё найденное значение коэффициента корреляции). - В ячейку А36 введите формулу: =B32-B31*КОРЕНЬ(1/(I5-3)) (находим нижнюю границу доверительного интервала для величины
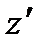 ).
). - В ячейку В36 введите формулу: =B32+B31*КОРЕНЬ(1/(I5-3) (находим верхнюю границу доверительного интервала для величины
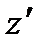 ).
). - В ячейку А40 введите формулу: =(EXP(2*A36)-1)/(EXP(2*A36)+1) (находим нижнюю границу доверительного интервала для коэффициента корреляции r по формуле
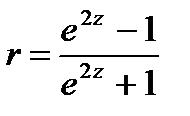 , подставляя в неё значение нижней границы доверительного интервала для
, подставляя в неё значение нижней границы доверительного интервала для 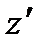 ).
). - В ячейку В40 введите формулу: =(EXP(2*B36)-1)/(EXP(2*B36)+1) (находим верхнюю границу доверительного интервала для r).
- Вы должны получить следующие результаты:
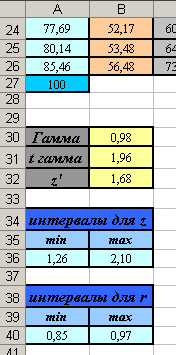
Вывод: с вероятностью 95% можно утверждать, что линейный коэффициент корреляции находится в пределах от 0,85 до 0,97.
- Спрогнозируем прирост прибыли предприятия, если затраты на модернизацию составят 100 тыс. руб.
- В ячейку А27 введите значение 100 (это прогнозное значение факторного признака Х).
- Из ячейки Е26 скопируйте формулу в ячейку Е27. В результаты вы получите искомое ожидаемое значение прироста прибыли (прогнозное значение результативного признака Y). Вы должны получить 68,97 тыс. руб.
Ожидаемый прирост прибыли при затратах на модернизацию производства в 100 тыс. руб. составляет 68,97 тыс. руб.
- Найдём доверительный интервал для прогнозного значения. Для этого нам будет нужно вычислить стандартную ошибку прогноза по формуле:
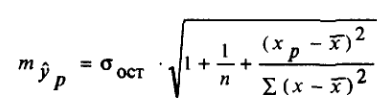 , где
, где 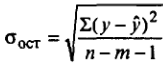 - остаточное среднее квадратическое отклонение.
- остаточное среднее квадратическое отклонение.
В случае линейной регрессии: m = 1 (в уравнении регрессии один параметр рядом с неизвестным).
Доверительные интервалы прогнозного значения определяются по формулам:
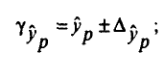
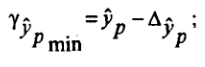
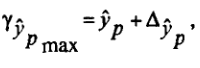 , где
, где
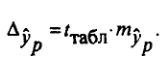
- Создайте заготовку таблицы для последующих вычислений (см. рисунок).
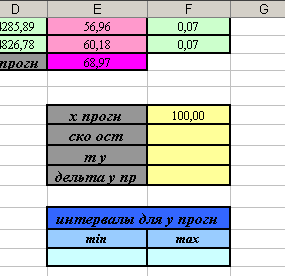
- Введите в ячейку F31 формулу: =КОРЕНЬ(СУММ(M2:M26)/(I5-2)) (находим величину
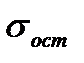 ).
). - Введите в ячейку F32 формулу: =F31*КОРЕНЬ(1+1/I5+((F30-I1)^2)/СУММ(L2:L26)) (находим стандартную ошибку прогноза).
- Введите в ячейку F33 формулу: =F32*I18 (находим величину
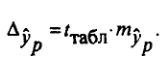 ).
). - Введите в ячейку Е37 формулу: =E27-F33 (находим нижнюю границу доверительного интервала).
- Введите в ячейку F37 формулу: =E27+F33 (находим верхнюю границу доверительного интервала).
- Вы должны получить следующие результаты:
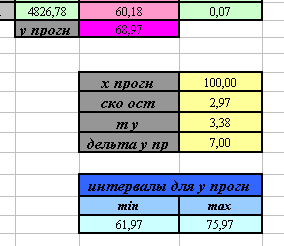
Вывод: с вероятность 95% при условии линейной зависимости между изучаемыми признаками можно утверждать, что при затратах на модернизацию производства в 100 тыс. руб. ожидаемый прирост прибыли будет в пределах от 61,97 тыс. руб. до 75,97 тыс.руб.
- Найдём средний коэффициент эластичности. Коэффициент эластичности показывает, на сколько процентов в среднем по совокупности изменится результат Y от своей величины при изменении фактора Х на 1% от своего значения. Он рассчитывается по формуле:
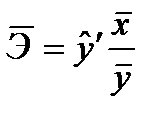
В нашем случае: 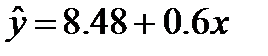 . Отсюда:
. Отсюда: 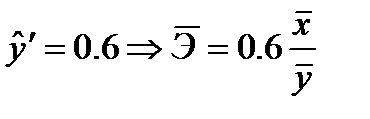 .
.
a. Сделайте заготовку таблицы (см. рисунок).
b. Введите в ячейку F39 формулу: =0,6*I1/I2. Вы должны получить результат Э = 0,78.
Вывод: при изменении значения признака Х (затрат на модернизацию) на 1% значение признака Y (прирост прибыли) в среднем изменится на 0,78%.
Квадратичная регрессия
Квадратичная регрессия задаётся уравнением:
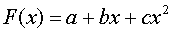 .
.
Параметры этой функции находятся из системы уравнений:
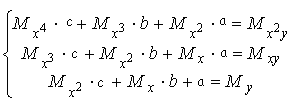 .
.
В этой системе:
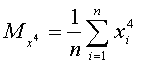
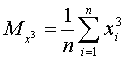
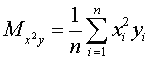
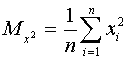
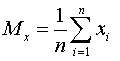
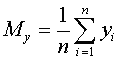
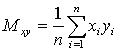
Таким образом, все эти параметры являются средними величинами.
- На новом листе книги MS Excel создайте таблицы для вычислений (см. рисунок).
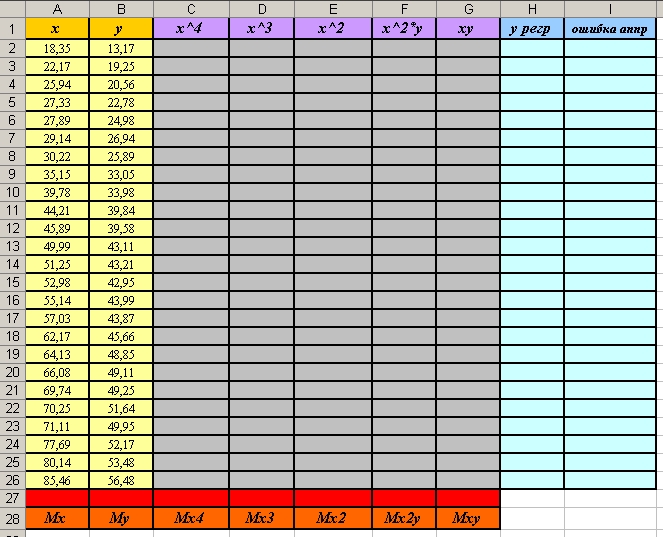
- В ячейку С2 введите формулу: =A2^4. Скопируйте эту формулу вниз в диапазон ячеек С3:С26.
- В ячейку D2 введите формулу: =A2^3. Скопируйте эту формулу вниз в диапазон ячеек D3:D26.
- В ячейку E2 введите формулу: =A2^2. Скопируйте эту формулу вниз в диапазон ячеек E3:E26.
- В ячейку F2 введите формулу: =E2*B2. Скопируйте эту формулу вниз в диапазон ячеек F3:F26.
- В ячейку G2 введите формулу: =A2*B2. Скопируйте эту формулу вниз в диапазон ячеек G3:G26.
- В ячейке А27 найдите значение величины
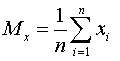 как среднее значение чисел из диапазона ячеек А2:А26 (используйте встроенную функцию MS Excel). Эту формулу скопируйте вправо в диапазон ячеек В27:G27 для того, чтобы получить значения остальных параметров системы уравнения (то есть в итоге будет подсчитано среднее значение для каждого столбца).
как среднее значение чисел из диапазона ячеек А2:А26 (используйте встроенную функцию MS Excel). Эту формулу скопируйте вправо в диапазон ячеек В27:G27 для того, чтобы получить значения остальных параметров системы уравнения (то есть в итоге будет подсчитано среднее значение для каждого столбца). - Вы должны получить следующую таблицу:
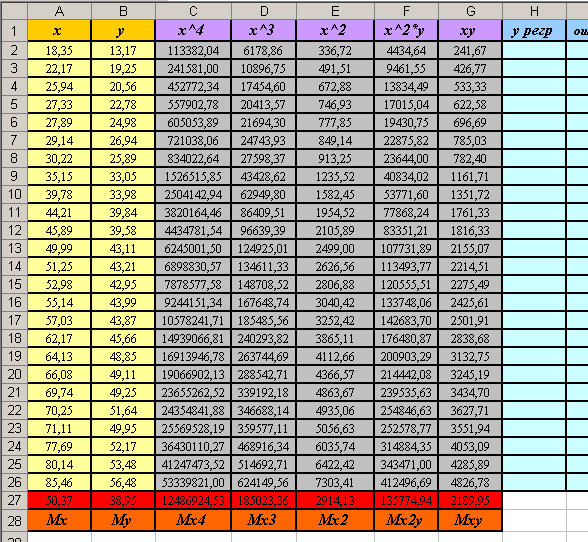
- Таким образом, нам требуется решить следующую систему уравнений:
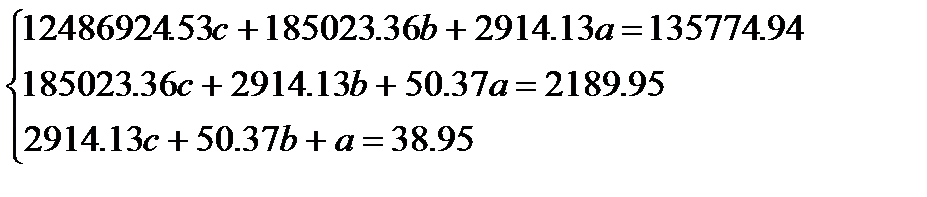
Эту систему уравнений можно записать в матричном виде:
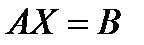
Здесь: А – матрица коэффициентов при неизвестных, Х – вектор-столбец неизвестных переменных, В – вектор-столбец свободных коэффициентов. Мы можем записать:
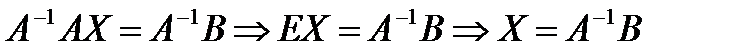 .
.
Следовательно, для того, чтобы найти неизвестные, нам нужно вычислить матрицу 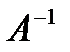 (матрица, обратная для матрицы А) и умножить её на вектор-столбец свободных коэффициентов. Полученный в результате этого умножения вектор столбец будет содержать искомые значения неизвестных.
(матрица, обратная для матрицы А) и умножить её на вектор-столбец свободных коэффициентов. Полученный в результате этого умножения вектор столбец будет содержать искомые значения неизвестных.
- Создайте заготовки таблиц для вычислений (см. рисунок).
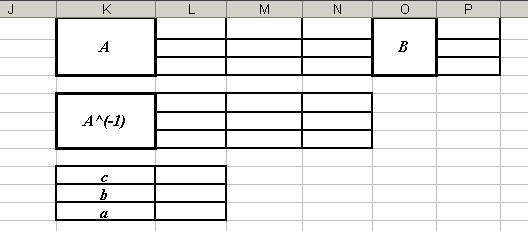
- Заполните данными матрицу А. Внимание: во избежание накопления погрешностей, связанных с округлением, создавать эту таблицу нужно следующим образом:
i. Установите курсор в ячейку L1 и задайте формулу: =C27. В результате в ячейку L2 будет подставлено точное вычисленной значение 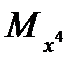 .
.
ii. Аналогичным образом заполните остальную таблицу, подставляя нужные значения параметров.
- Таким же образом задайте значения вектора-столбца свободных коэффициентов В.
- Найдём матрицу
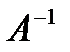 . Выделите диапазон ячеек L5:N7 и вызовите пункт меню Вставка/Функция. В открывшемся диалоговом окне укажите категорию функций Математические и выберите функцию МОБР ( ). В новом диалоговом окне задайте в качестве массива диапазон ячеек L1:N3. Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив).
. Выделите диапазон ячеек L5:N7 и вызовите пункт меню Вставка/Функция. В открывшемся диалоговом окне укажите категорию функций Математические и выберите функцию МОБР ( ). В новом диалоговом окне задайте в качестве массива диапазон ячеек L1:N3. Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив). - Для того, чтобы вычислить значения параметров с, b и а, умножим матрицу
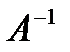 на вектор-столбец В (именно в таком порядке). Выделите диапазон ячеек L9:L11 и вызовите пункт меню Вставка/Функция. В открывшемся диалоговом окне укажите категорию функций Математические и выберите функцию МУМНОЖ ( ). В открывшемся диалоговом окне в качестве Массива 1 задайте диапазон ячеек L5:N7 (матрица
на вектор-столбец В (именно в таком порядке). Выделите диапазон ячеек L9:L11 и вызовите пункт меню Вставка/Функция. В открывшемся диалоговом окне укажите категорию функций Математические и выберите функцию МУМНОЖ ( ). В открывшемся диалоговом окне в качестве Массива 1 задайте диапазон ячеек L5:N7 (матрица 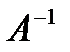 ), а в качестве Массива 2 задайте диапазон ячеек Р1:Р3 (вектор-столбец В). Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив).
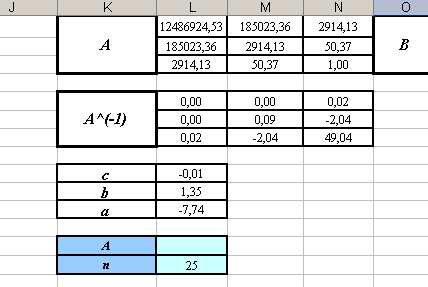
), а в качестве Массива 2 задайте диапазон ячеек Р1:Р3 (вектор-столбец В). Нажмите одновременно клавиши Ctrl+ Shift+ Enter (мы обрабатываем диапазоны ячеек как единый массив). - Вы должны получить следующие результаты:
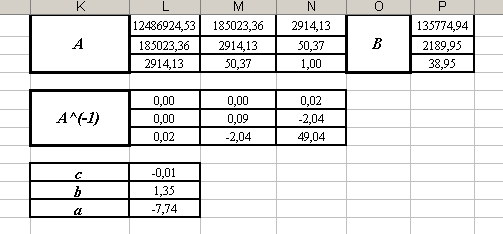
Уравнение квадратичной регрессии имеет вид: 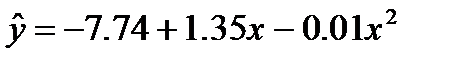
- Построим график квадратичной регрессии и график эмпирической функции в одной системе координат.
- Вычислим теоретические значения прироста прибыли, используя полученное уравнение квадратичной регрессии (подставим значения признака Х в полученное уравнение квадратичной регрессии). Установите курсор в ячейку Н1 и введите формулу: =$L$11+$L$10*A2+$L$9*A2*A2. Скопируйте эту формулу в диапазон ячеек Н2:Н26.
- Выделите два несмежных диапазона А2:А26 и Н2:Н26 (для выделения несмежных диапазонов удерживайте нажатой клавишу Ctrl).
- Вызовите пункт меню Вставка/Диаграмма. В открывшемся диалоговом окне выберите тип диаграммы – точечная. Нажмите кнопку Готово. Вы должны получить следующий график:
- Скройте легенду.
- Двойным щелчком на маркерах построенной диаграммы вызовите окно свойств. В этом окне в левой его части установите тип линии – обычная (вместо отсутствует).
- Выделите диаграмму и в пункте меню Диаграмма выберите пункт Добавить данные.
- В открывшемся диалоговом окне задайте диапазон В2:В26. Нажмите ОК.
- Задайте для диаграммы заголовок и подписи осей.
- Найдём среднюю ошибку аппроксимации уравнения линейной регрессии по формуле:
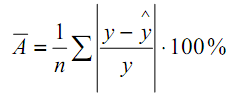
Средняя ошибка аппроксимации должна быть не больше 10% - 12%.
- Создайте заготовку таблицы (см. рисунок). Для ячейки L13 установите процентный формат.
- Установите курсор в ячейку I2 и введите формулу: =ABS((B2-Н2)/B2). Скопируйте эту формулу вниз в диапазон ячеек I3:I26.
- Введите в ячейку L13 формулу: =СУММ(I2:I26)/L14 (вычисляем стандартную ошибку аппроксимации по формуле).
- Вы должны получить стандартную ошибку аппроксимации 3,35%, это означает, что использование квадратичной регрессии в данном случае допустимо.
- Оценим тесноту связи с помощью индекса корреляции, который вычисляется по формуле:
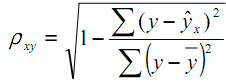
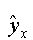 - теоретические значения результативного признака, вычисленные с помощью уравнения регрессии.
- теоретические значения результативного признака, вычисленные с помощью уравнения регрессии.
- Сделайте заготовки таблиц для последующих вычислений (см. рисунок).
- В ячейке S2 вычислите среднее значение результативного признака – значений прибыли (диапазон ячеек В2:В26).
- Установите курсор в ячейку U2 и введите формулу: =(B2-$S$1)^2. Скопируйте эту формулу вниз в диапазон ячеек U3:U26 (находим величину
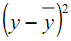 ).
). - В ячейку V2 введите формулу: =(B2-H2)^2. Скопируйте эту формулу вниз в диапазон ячеек V3:V26 (находим величину
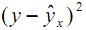 ).
). - В ячейках U27 и V27 подсчитайте сумму значений соответствующих столбцов.
- Установите курсор в ячейку S3 и введите формулу: =КОРЕНЬ(1-V27/U27) (вычисляем индекс корреляции по формуле).
- Вы должны получить следующие результаты:
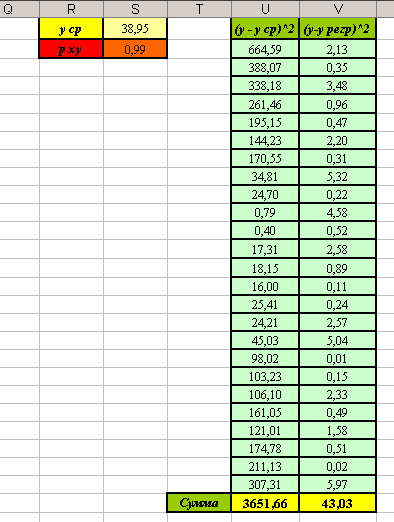
Вывод: индекс корреляции 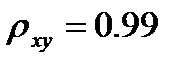 , следовательно, связь между признаками очень тесная.
, следовательно, связь между признаками очень тесная.
- Оценим значимость параметров уравнения квадратичной регрессии и индекса корреляции. Для этого будем использовать критерий Фишера: нам нужно будет сравнить фактическое значение критерия и табличное. Фактическое значение критерия рассчитывается по формуле:
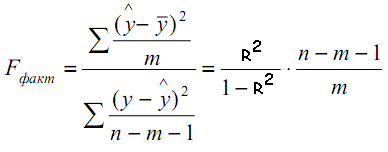
В этой формуле: n – объём совокупности, m – число параметров при переменных. В нашем случае таких параметров два: b и c (параметр а является свободным коэффициентом).
Табличное значение F-критерия определяется для заданного уровня значимости 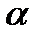 и степенях свободы k1 = m и k2 = n – m – 1.
и степенях свободы k1 = m и k2 = n – m – 1.
a. Создайте заготовку таблицы для вычислений (см. рисунок).
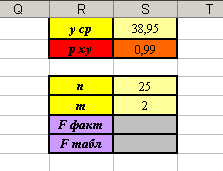
b. Установите курсор в ячейку S6 и введите формулу: =(S4-S5-1)*S2*S2/(S5*(1-S2*S2)) (вычисляем фактическое значение F-критерия по формуле, подставляя нужные значения из ячеек на листе).
c. Получим табличное значение F-критерия с помощью встроенной функции для уровня значимости 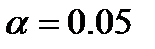 и степеней свободы k1 = 2 и k2= n– m–1 =25–2–1=22. Установите курсор в ячейку S7 и вызовите пункт меню Вставка/Функция. Укажите категорию функций Статистические и выберите функцию FРАСПРОБР ( ). В открывшемся диалоговом окне укажите вероятность 0.05 (это уровень значимости
и степеней свободы k1 = 2 и k2= n– m–1 =25–2–1=22. Установите курсор в ячейку S7 и вызовите пункт меню Вставка/Функция. Укажите категорию функций Статистические и выберите функцию FРАСПРОБР ( ). В открывшемся диалоговом окне укажите вероятность 0.05 (это уровень значимости 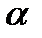 ), Степень_свободы1 – ячейка S5, Степень_свободы2 – S4-S5-1.
), Степень_свободы1 – ячейка S5, Степень_свободы2 – S4-S5-1.
d. Вы должны получить следующие результаты:
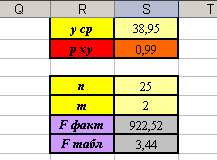
Вывод: 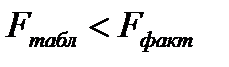 - следовательно, гипотеза о случайной природе оцениваемых величин отвергается, и с вероятностью 95% можно утверждать, что параметры уравнения регрессии и индекс корреляции являются значимыми.
- следовательно, гипотеза о случайной природе оцениваемых величин отвергается, и с вероятностью 95% можно утверждать, что параметры уравнения регрессии и индекс корреляции являются значимыми.
- Спрогнозируем прирост прибыли предприятия, если затраты на модернизацию составят 100 тыс. руб.
- В ячейку А29 введите значение 100.
- Из ячейки Н26 скопируйте формулу в ячейку Н29. В результаты вы получите искомое ожидаемое значение прироста прибыли. Вы должны получить 53,8 тыс. руб.
Ожидаемый прирост прибыли при затратах на модернизацию производства в 100 тыс. руб. составляет 53,8 тыс. руб.
- Найдём коэффициент эластичности. Он рассчитывается по формуле:
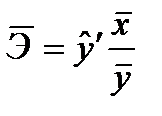
В нашем случае: 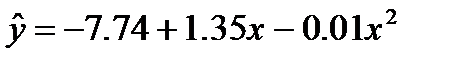 . Отсюда:
. Отсюда: 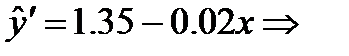
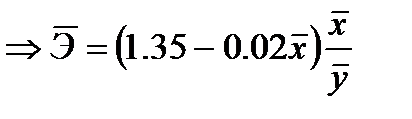 .
.
a. Сделайте заготовку таблицы (см. рисунок).
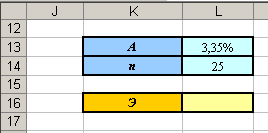
b. Введите в ячейку L16 формулу: =(1,35-0,02*A27)*A27/B27. Вы должны получить результат Э = 0,44.
Вывод: при изменении значения признака Х (затрат на модернизацию) на 1% значение признака Y (прирост прибыли) в среднем изменится на 0,44%.








