Порядок оформления лабораторной работы

Дата: 2025-06-02; Просмотры: 19
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО РЫБОЛОВСТВУ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«МУРМАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(ФГОУ ВПО «МГТУ»)

 

Кафедра Информационных систем

и прикладной математики

 

 

Методические указания

к лабораторным работам

 

 

по дисциплине

Эконометрика

название дисциплины

для направления подготовки (специальности)

 080100 «экономика»

код направления подготовки

для программы специализированной подготовки магистра

наименование направления подготовки

Составитель

Яретенко Николай Иванович

 

Доцент кафедры ИС и ПМ
         

 

Мурманск

2013

ОГЛАВЛЕНИЕ

 

ОБЩИЕ ОРГАНИЗАЦИОННО - МЕТОДИЧЕСКИЕ УКАЗАНИЯ………………………...3

 

ЛАБОРАТОРНАЯ РАБОТА № 1. Вариационные ряды, описательная статистика…………………………………….4

 

ЛАБОРАТОРНАЯ РАБОТА № 2. Корреляционно-регрессионный анализ …… 11

 

ЛАБОРАТОРНАЯ РАБОТА № 3. Множественная егрессия.Гетероскедастичность и гомоскедастичность остатков…… …47

 

ЛАБОРАТОРНАЯ РАБОТА № 4. Анализ временных рядов……………… ....98

 

ЛАБОРАТОРНЫЕ РАБОТЫ ДЛЯ САМОПОДГОТОВКИ

 

ЛАБОРАТОРНАЯ РАБОТА № 1д. Проверка гипотезы о нормальном распределении……………………………..112

 

ЛАБОРАТОРНАЯ РАБОТА № 2д. Оценивание параметров случайной величины………………………….……..…120

 

 

Общие организационно-методические указания

С основными методологическими положениями данного курса сту­денты знакомятся на обзорных лекциях. Материалы лекций и самостоятельная подготовка составля­ют основу для проведения практических занятий по решению типо­вых задач и лабораторных занятий с использованием ПЭВМ.

В качестве инструментального средства для решения эконометрических задач применяется EXCEL (так же возможно применение и специальных программных продуктов SPSS, VSTAT, Matrixer и др.).

Порядок оформления лабораторной работы

 

Лабораторная работа выполняется на ПЭВМ в компьютерном классе с использованием установленных программных средств и защищается в установленные преподавателем сроки.

Титульный лист лабораторной работы должен содержать все необходимые реквизиты: названия Университета и кафедры; наименование учебной дисциплины; номер (наименование) группы и номер зачетной книжки, Ф.И.О. студента и преподавателя.

Работа без указания номера зачетной книжки проверке не подлежит, при отсутствии Ф.И.О. преподавателя установленные им сроки проверки работы могут быть нарушены.

Решение задач лабораторной работы должно сопровождаться необходимыми комментариями, т.е. все основные моменты процесса решения задачи должны быть раскрыты и обоснованы на основе соответствующих теоретических положений.

К защите допускаются студенты, выполнившие правильно и в полном объеме Лабораторную работу.

Для получения зачета по результатам собеседования студент должен знать теоретические основы по тематике лабораторной работы и уметь ответить на конкретные вопросы по содержанию проверенной работы.

Номер Вашего варианта соответствует последней цифре зачетной книжки (если преподавателем не задан другой порядок выбора варианта).

Лабораторная работа №1

Вариационные ряды, описательная статистика

Задание

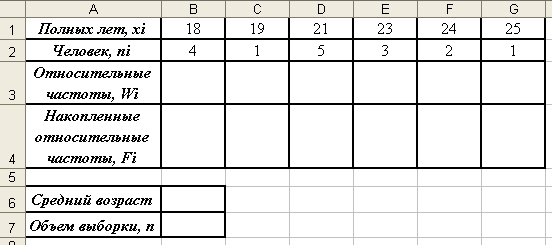
В некотором магазине в течение часа производился опрос покупателей: у каждого покупателя спрашивался его возраст (количество полных лет). Были получены следующие данные:

Полных лет 18 19 21 23 24 25
Человек 4 1 5 3 2 1

 

Требуется найти средний возраст покупателей, построить полигон относительных частот и кумуляту.

Решение:

В данной задаче имеет место дискретная случайная величина – возраст покупателя.

Обозначим эту случайную величину Х.

В первой строке таблицы находятся варианты – возможные значения случайной величины Х, во второй строке находятся частоты.

Для того, чтобы построить требуемые графики, необходимо будет найти относительные частоты и накопленные относительные частоты.

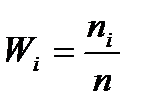- относительные частоты; 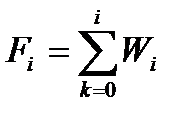- накопленные относительные частоты;

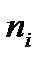- частоты; 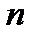- общее количество наблюдений, оно равно сумме всех наблюдений.

Находить средний возраст покупателей в данной задаче следует по формуле средней взвешенной:

 

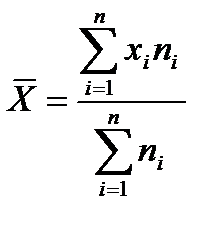
Выполнение задания с помощью приложения MS Excel :

  1. Запустите приложение MS Excel;
  2. В верхней части первого листа создайте таблицу с исходными данными так, как это показано на рисунке ниже:

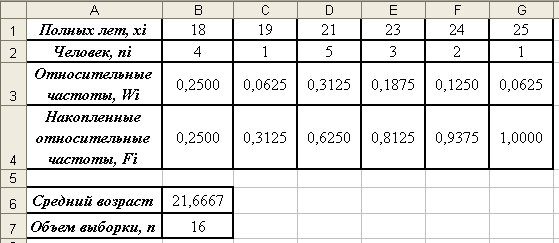
  1. Найдем средний возраст покупателей, используя встроенную функцию MS Excel. Установите курсор в ячейку В6 и введите формулу: =СРЗНАЧ(В1:G1);
  2. Вычислим объем выборки: установите курсор в ячейку В7 и введите формулу: =СУММ(В2:G2);
  3. Вычислим относительные частоты. Установите курсор в ячейку В3 и введите формулу: =B2/$B$7. Скопируйте эту формулу в диапазон ячеек C3:G3.
  4. Вычислим накопленные относительные частоты:
    1. Введите в ячейку В4 формулу: =В3;
    2. В ячейку С4 введите формулу: =B4+C3;
    3. Скопируйте формулу из ячейки С4 в диапазон ячеек D4:G4;
  5. Если все выполнено верно, то таблица должна выглядеть следующим образом:

  1. Построим полигон относительных частот. Для этого нам нужно построить график на основании данных, находящихся в диапазоне В3:G3. Выделите этот диапазон и выполните следующие действия:
    1. Выполните пункт меню Вставка/Диаграмма;
    2. В открывшемся диалоговом окне выберите: тип диаграммы – график; вид диаграммы – график с маркерами. Нажмите Далее.
    3. В новом диалоговом окне перейдите на вкладку Ряд. На этой вкладке в нижней части окна найдите поле Подписи оси Х и задайте в этом поле диапазон В1:G1. Это означает, что по оси Х будут подписаны данные из первой строки таблицы, то есть будет указан возраст покупателей. Нажмите Готово. Вы должны получить следующий график:

  1. Аналогичным образом самостоятельно постройте кумуляту (данные для построения графика находятся в диапазоне В4:G4, данные для подписи оси Х – в диапазоне В1:G1). График должен иметь следующий вид:

Задание 2

В магазине в течение 10 дней подсчитывали количество проданного товара заданного вида. В результате были получены следующие данные:

12 15 16 12 17 11 15 12 10 12

Для полученного вариационного ряда определить:

Решение:

В данной задаче имеет место несгруппированный вариационный ряд.

Размах ряда определяется по формуле: 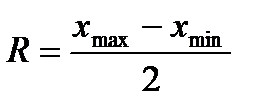, дисперсия - 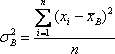, среднее квадратическое отклонение - 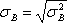, коэффициент вариации - .

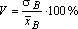Моду и медиану находят в ранжированном ряде (отсортированном по возрастанию или убыванию).

Медианой называется значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части. Если выборка содержит четное число членов, то медианой в этом случае принято среднее арифметическое значений, расположенных в центре ряда.

 

Мода – такая величина признака в изучаемом вариационном ряду, которая встречается чаще всего.

 

Выполнение задания с помощью приложения MS Excel :

  1. Запустите приложение MS Excel, откройте тот файл, в котором выполнялось предыдущее задание, и перейдите на второй лист;
  2. В верхней части первого листа создайте таблицу с исходными данными так, как это показано на рисунке ниже:

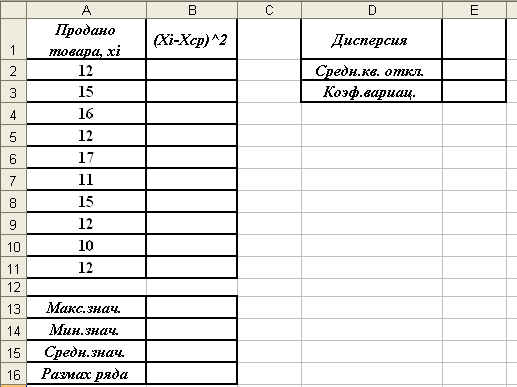
  1. Найдем максимальное значение признака. Установите курсор в ячейку В13 и введите формулу: =МАКС(A2:A11);
  2. Аналогичным образом в ячейке В4 определите минимальное значение признака (функция МИН(диапазон ячеек));
  3. В ячейке В15 найдите среднее значение признака, используя функцию СРЗНАЧ(диапазон ячеек);
  4. В ячейке В16 вычислим размах ряда по формуле: =(B13-B14)/2.
  5. Найдем дисперсию, для этого проведем дополнительные вычисления.
    1. Установите курсор в ячейку В2 и введите формулу: =СТЕПЕНЬ((A2-$B$15);2). Скопируйте эту формулу вниз в диапазон ячеек В3:В11.
    2. Теперь можно вычислить саму дисперсию. Установите курсор в ячейку Е1 и введите формулу: =СУММ(B2:B11)/10;
  6. Вычислим среднее квадратическое отклонение. Установите курсор в ячейку Е2 и введите формулу: =КОРЕНЬ(E1);
  7. Вычислим коэффициент вариации. Курсор в ячейку Е3 и введите формулу: =E2/B15. Установите для этой ячейки процентный формат (Вид/Формат ячейки, в открывшемся диалоговом на первой вкладке Число выбрать Вид – Процентный);
  8. В итоге таблица с вычислениями должна иметь следующий вид:

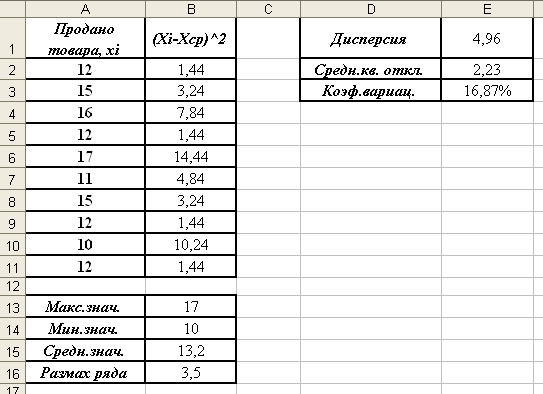
  1. Вычислим значение дисперсии с помощью встроенной функций MS Excel. Установите курсор в ячейку F1 и введите формулу: =ДИСПР(A2:A11). Данная функция позволяет вычислить дисперсию выборки. Вычисленное значение должно совпасть с тем, что вы получили при вычислениях «вручную».
  2. Для поиска медианы ряд его нужно ранжировать, то есть отсортировать. Отсортируем ряд по возрастанию. Установите курсор в ячейку А1 и выполните пункт меню Данные/Сортировка… В открывшемся диалоговом окне должен стоять флажок Сортировать по возрастанию, нажмите ОК. Обратите внимание, что вместе с первым столбцом будет соответственно отсортирован и второй столбец. Значения вычисленных величин не изменятся.

 

  1. Дополнительно оформите таблицу на листе так, как это показано на рисунке ниже:

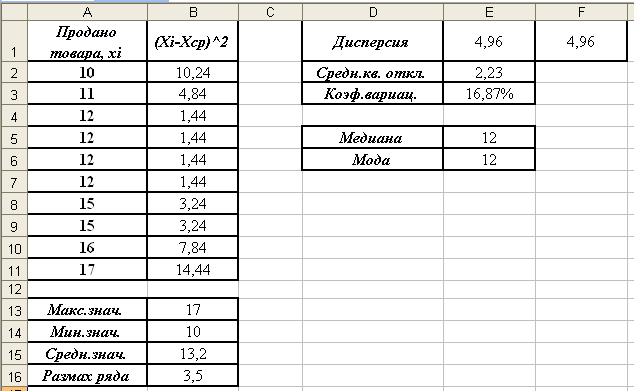
  1. Установите курсор в ячейку Е5 и введите формулу: =МЕДИАНА(A2:A11);
  2. Установите курсор в ячейку Е6 и введите формулу: =МОДА(A2:A11);
  3. В результате всех вычислений, таблица должна иметь следующий вид:

 

Контрольные вопросы к заданиям

  1. Объясните смысл всех статистических величин, вычисленных при выполнении обоих заданий.
  2. Расскажите, какие встроенные функции MS Excel были использованы при выполнении заданий. Для чего эти функции используются?
  3. Является ли выборка из задания 2 однородной? Почему?

 

Задания для самостоятельного выполнения

  1. Используя исходные данные из задания 2 составьте ряд распределения для случайной величины (вы должны получить таблицу, аналогичную той, что дана в условии задания 1). Постройте полигон относительных частот и кумуляту.
  2. На новом листе книги MS Excel выделите в диапазоне ячеек А1:А10 (в столбец) введите следующие данные:

2k+1 2k+3 2k-1 2k 2k+2 2k+3 2k-4 k+9 2k 2k-5

 

k – последняя цифра зачетной книжки.

Для полученного вариационного ряда вычислите:

· Размах ряда;

· Среднее значение;

· Дисперсию;

· Среднее квадратическое отклонение;

· Коэффициент вариации;

· Медиану;

· Моду.

 

Лабораторная работа №2

Корреляционно-регрессионный анализ

Задание

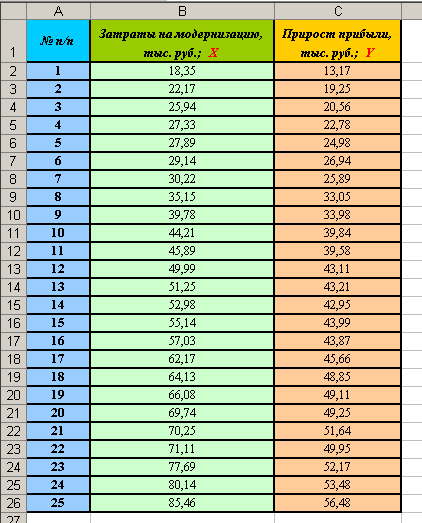
Для 25 однотипных предприятий имеются данные о затратах на модернизацию производства и о приросте прибыли.

№ п/п Затраты на модернизацию, тыс. руб. Прирост прибыли, тыс. руб.
1 18,35 13,17
2 22,17 19,25
3 25,94 20,56
4 27,33 22,78
5 27,89 24,98
6 29,14 26,94
7 30,22 25,89
8 35,15 33,05
9 39,78 33,98
10 44,21 39,84
11 45,89 39,58
12 49,99 43,11
13 51,25 43,21
14 52,98 42,95
15 55,14 43,99
16 57,03 43,87
17 62,17 45,66
18 64,13 48,85
19 66,08 49,11
20 69,74 49,25
21 70,25 51,64
22 71,11 49,95
23 77,69 52,17
24 80,14 53,48
25 85,46 56,48

Выполнение работы

Внимание! При создании таблиц используйте в качестве образца таблицы, приведённые на рисунках, при этом вы должны вводить данные в те же ячейки, что и на рисунке (столбцы и номера строк должны совпадать). В противном случае вычисления по формулам, данным в работе, будут неверными.

Построение поля корреляции, определение вида регрессии

  1. Создайте новую книгу MS Excel;
  2. На первом листе создайте таблицу с исходными данными (см. рисунок):

  1. Построим поле корреляции:
    1. Выделите диапазон ячеек В2:С26.
    2. Вызовите пункт меню Вставка/Диаграмма…
    3. В открывшемся диалоговом окне выберите вид диаграммы – Точечная, нажмите кнопку Готово.
    4. На текущий лист будет добавлена диаграмма:

    1. Для этой диаграммы скройте легенду, добавьте подписи осей, добавьте название.

  1. Определим вид приближающей регрессии. По полю корреляции можно предположить, что это может быть линейная, степенная или логарифмическая функция. MS Excel позволяет добавлять в диаграммы линии тренда (кривые приближающих функций), эта возможность позволяет пользователю более точно определить вид регрессии.
    1. Выделите диаграмму (щёлкните на ней левой кнопкой мыши).
    2. В главном меню окна должен появиться пункт Диаграмма. Выберите в этом пункте подпункт Добавить линию тренда.
    3. В открывшемся диалоговом окне выберите тип линии тренда – линейная. Нажмите кнопку ОК. В результате линия тренда будет добавлена на диаграмму. По полученному графику можно предположить, что линейная регрессия может быть использована в данном случае.

    1. Аналогичным образом добавьте на эту же диаграмму ещё одну линию тренда – логарифмическую. По графику будет видно, что логарифмическая регрессия достаточно хорошо отражает зависимость величин.

    1. Аналогичным образом добавьте на эту же диаграмму ещё одну линию тренда – полиномиальную, степень – 2 (это будет график квадратичной регрессии). По графику видно, что квадратичная регрессия так же может быть использована в данном случае (её график практически совпадёт с графиком логарифмической регрессии).

    1. Можно так же добавить на диаграмму экспоненциальную и степенную линии тренда, но для них сразу можно сделать вывод о том, что эти типы регрессий не подходят в данном случае.

Вывод: Для имеющихся данных следует использовать линейную, квадратичную или логарифмическую регрессию.