Самостоятельная работа № 1
Тема: Решение задач линейной алгебры и аналитической геометрии.
Кол-во часов: 3 часа.
Задание: выполнить задания.
Вид самостоятельной работы студента: решение задач.
Цель работы: способствовать развитию навыков самостоятельного применения знаний при выполнении действий с матрицами и определителями, решения СЛУ разными методами, составления уравнений прямых на плоскости и кривых второго порядка.
Форма контроля: проверка выполненных заданий преподавателем.
ВАРИАНТ 1
1. Даны матрицы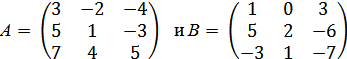 
.
Найдите: 1) 3А + 2В; 2) АВ; 3)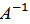 
; 4) определитель матрицы А.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. Даны координаты вершин треугольника АВС: A (1; -1), B (4; 3), C (5; 1).
Найти:
1. уравнения сторон треугольника и их угловые коэффициенты;
2. величину угла наклона прямой АВ к оси абсцисс, а также величины
внутренних углов треугольника;
3. уравнения высот треугольника и координаты точки Р из пересечения;
4. длину медианы АМ треугольника;
5. уравнение прямой, проходящей через точку Р параллельно прямой АС
6. Построить заданный треугольник и все линии в системе координат.
4. Составить уравнение окружности проходящей через точки A (0; 2), B (1; 1),
C (2; -2).
5. Составить каноническое уравнение эллипса, если даны его вершины (0; 3)
и (0; -3), расстояние между фокусами равно 8.
6. Составить каноническое уравнение гиперболы с фокусами на оси Ox, проходящей через точки M1 (-6; -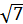 
); M2 ( 
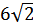; 4).
7. Составить уравнение параболы с вершиной в начале координат, фокус которой находится в точке пересечения прямой 3x-2y+5=0 с осью ординат.
8. Привести уравнение кривой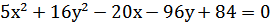 
к каноническому виду и постройте её.
ВАРИАНТ 2
1. Даны матрицы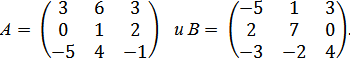 
Найдите: 1) 2А – 3В; 2) ВА; 3)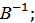 
4) определитель матрицы А.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. Даны координаты вершин треугольника АВС: A (0;-1), B (3; 3), C (4; 1).
Найти:
1. уравнения сторон треугольника и их угловые коэффициенты;
2. величину угла наклона прямой АВ к оси абсцисс, а также величины
внутренних углов треугольника;
3. уравнения высот треугольника и координаты точки Р из пересечения;
4. длину медианы АМ треугольника;
5. уравнение прямой, проходящей через точку Р параллельно прямой АС
6. Построить заданный треугольник и все линии в системе координат.
4. Составить уравнение окружности, касающейся оси абсцисс в точке A (2; 0) и проходящей через точку B (-1; 3).
5. Найти длины осей, координаты фокусов и эксцентриситет эллипса
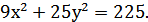
6. Составить каноническое уравнение гиперболы, если 2c = 10, 2a = 6.
7. Определить координаты фокуса и составить уравнение директрисы параболы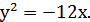 
8. Привести уравнение кривой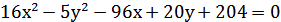 
к каноническому виду и постройте её.
ВАРИАНТ 3
1. Даны матрицы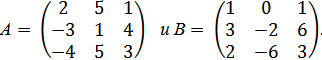 
Найдите: 1) 3В – 2А; 2) АВ; 3) 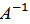; 4) определитель матрицы В.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. В треугольнике АВС известны вершины А(-4;2), В(3;3) и точка пересечения его медиан М(2;1). Определить:
1. вершину С;
2. уравнение стороны (АС);
3. угол С;
4. уравнение высоты (ВК);
5. длину стороны (АВ).
4. Составить уравнение прямой, проходящей через центры окружностей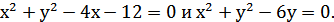 
5. Составить каноническое уравнение эллипса, фокусы которого
расположены на оси Ox, симметрично относительно начало координат, проходящего через точки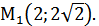 
Малая ось его равна 6.
6. Составить каноническое уравнение гиперболы, если эксцентриситет ε = 1,25, а действительная ось - 2a = 16.
7. Найти вершину, фокус, ось и директрису параболы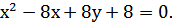 
8. Привести уравнение кривой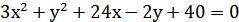 
к каноническому виду и постройте её.
ВАРИАНТ 4
1. Даны матрицы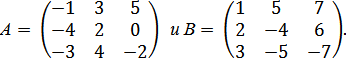 
Найдите: 1) 3А + 2В; 2) ВА; 3) 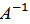; 4) определитель матрицы В.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. Треугольник АВС задан своими вершинами А(2;3), В(6;9) и С(9;-2). Определить:
1. точку пересечения медиан;
2. уравнение стороны (АВ);
3. угол В;
4. уравнение высоты (АF);
5. площадь треугольника.
4. Составьте уравнение окружности, проходящей через точки А(8; 5) и В(-1; -4) и имеющей центр на оси абсцисс.
5. Составьте уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно 20, а эксцентриситет равен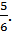 
6. Составьте уравнение гиперболы, если эксцентриситет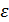 
= 1,5, а расстояние между фокусами 2с = 6.
7. Составьте уравнение параболы, у которой расстояние фокуса от вершины равно 3.
8. Привести уравнение кривой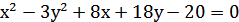 
к каноническому виду и постройте её.
ВАРИАНТ 5
1. Даны матрицы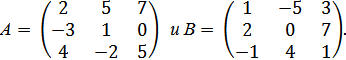 
Найдите: 1) 2А + 3В; 2) АВ; 3)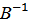 
; 4) определитель матрицы А.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. Дан квадрат АВСD, у которого известны три вершины А(-3;1), В(1;4), С(0;-3)
Определить:
1. вершину D;
2. уравнение стороны (СD);
3. уравнение стороны (ВD);
4. уравнение стороны (АС);
5. точку пересечения диагоналей.
4. Составьте уравнение окружности радиусом R = 5, центр которой находится в точке С(-1; 3).
5. Составьте уравнение эллипса с фокусами на оси Ох, если сумма полуосей равна 25, а фокусы имеют координаты (-5; 0) и (5; 0).
6. Составьте уравнение гиперболы, если координаты фокусов (-5; 0) и (5; 0), а уравнения асимптот у =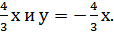 
7. Составить уравнение параболы, если дан фокус F(- 7; 0) и уравнение директрисы х – 7 = 0.
8. Привести уравнение кривой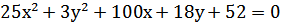 
к каноническому виду и постройте её.
ВАРИАНТ 6
1. Даны матрицы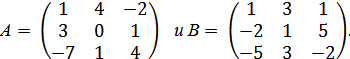 
Найдите: 1) 3В – 2А; 2) ВА; 3) 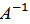; 4) определитель матрицы В.
2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.
3. Вершины треугольника находятся в точках А(3; -4), В(1; 3) и С(-4; -2).
Определить:
1. уравнение высоты (СD);
2. уравнение стороны (ВС);
3. угол В;
4. площадь треугольника;
5. уравнение медианы (АМ).
4. Составить уравнение окружности радиусом R = 3, центр которой находится в точке С (2; - 3).
5. Дан эллипс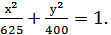 
Найдите его эксцентриситет.
6. Составьте уравнение гиперболы по уравнениям ее асимптот у =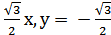 
и координатам точки, через которую проходит гипербола (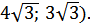 
7. Дана парабола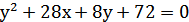 
. Составьте уравнение ее директрисы.
8. Привести уравнение кривой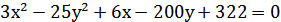 
к каноническому виду и постройте её.