.43.Силы в зацеплении прямозубой конической передачи.
В отличии от прямозубой конической передачи передачи с круговыми зубьями,осевая сила на шестерне 
не всегда направлена к большему основанию конуса.В данном случае её направление зависит от того совпадает ли направление линии зуба на шестерне с направлением её вращения если смотреть на шестерню с вершины делительного конуса.
Направление линии и направление вращения совпадают в следующих случаях:
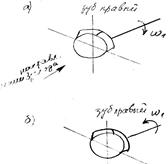
Направление линии зуба и направление вращения не совпадают:
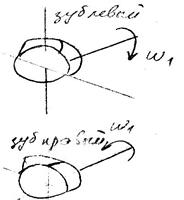
Для шестерни: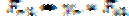 
, 
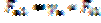
-коэффициент радиальной силы
коэффициент осевой силы
Когда направление линии зуба не совпадает с направлением вращения шестерни коэф 
могут оказаться со знаком минус.
Направление векторов 
в зависимости от полученного знака: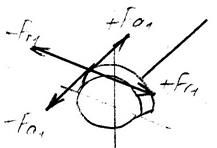 
Если 
тогда - 
тогда + 
45.Приведение конического зубчатого колеса с прямыми и круговыми зубьями к эквивалентному прямозубому цилиндрическому.
В конической передаче в каждом сечении зуба размеры этого сечения различны.С целью упрощения расчёта конические зубчатые колёса заменяют условными эквивалентными прямозубыми цилиндрическими с размерами зуба соответствующие размерам зубьев конических колёс на середине венца.
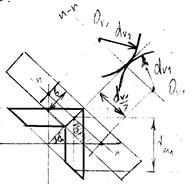
-центр эквивален. цилиндрической шестерни
- центр эквивален. Цилиндрич колеса
-делит диаметр эквивалентной цилиндрич шестерни
, 
-средн делит диаметр реальн шестерни колеса
, 
-число зубьев эквивал шестерни
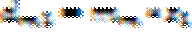-число зубьев реальн шестерни
, 
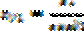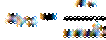
Конические передачи с круговыми зубьями
В данном случае используют двойное приведение.В начале коническое зубч колесо с круговыми зубьями приводят к эквивалентному цилиндр. С косыми зубьями ,а затем последние-к эквивалент цилиндр с прямыми зубьями получая так называемые биэквивалентные зубчатые колёса с числом зубьев:
, 
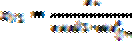46._ЧЕРВЯЧНЫЕ ПЕРЕДАЧИ
| Передача вращением между перекрещивающимися валами посредством червяка и сопряженного с ним колеса. |
Червяк – винт с трапециидальной или близкой по форме резьбой
Виды цилиндрических червяков
Бывают линейчатые и нелинейчатые. Линейчатые образуются винтовым движением прямой линии, а нелинейчатые винтовым движением конической или тороидальной формы.
К линейчатым относится 3 типа:
1. Архимедов ZA
2. Эвольвентный ZJ
3. Конвалютный ZN
47.Достоинства червячной передачи
– Возможность получения больших передаточных отношений
– Большая плавность работы
– Малая шумность
– Компактность
48.Недостатки червячной передачи
– Большое трение в передачах Þ большой нагрев из-за, большого скольжения, что требует применения дорогостоящей оловянной бронзы
– Очень низкий КПД (60-95%)
– Износ зубьев
– Мощность не выше 50 кВт
49. Геометрия червячной передачи
Червяк является ведущим, колеса ведомым. Червячная передача бывает следующих типов:
1. Цилиндрическая – делительная и начальная поверхности червяка и колеса круговые цилиндры.
2. Глобоидные – делительная поверхность является частью вогнутой поверхности тора (глобоида)
| Нагрузочная способность червяка выше за счет увеличения числа зубьев колеса, находящего в зацеплении с витками червяка. |
m – осевой модуль червяка
p = p×m – расчетный осевой шаг червяка
pX = p × z1 – ход витка (шаг винтовой линии)
g = arctg (pX / pd1) – делительный угол подъема линии витка
Делительный диаметр червяка:
d1 = m×z1 / tg g, причем z1 / tg g = q – коэффициент диаметра червяка.
d2 = mz2 – число зубьев колеса
a = (d1 + d2) / 2 – межосевое расстояние
Кинематика червячных передач
U = w1/w2 = n1/n2 = z2/z1
За 1 оборот червяк повернется на угол y, а колесо на угол y2 = y × pX / pd2.
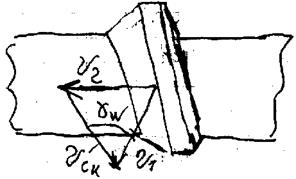
V1 – окружная скорость червяка на диаметре dW1, V2 – окружная скорость колеса на диаметре dW2, gW – начальный угол подъема витка
50. Понятие о смещении в червячной передаче
Смещение червячной передачи применяется с целью получения стандартного межосевого расстояния
