Тема урока: Шестнадцатеричная система счисления. Перевод чисел из шестнадцатеричной системы в двоичную, восьмеричную и десятичную системы и обратно.
7 октября 2022 г.
Классная работа
Тема урока: Шестнадцатеричная система счисления. Перевод чисел из шестнадцатеричной системы в двоичную, восьмеричную и десятичную системы и обратно.
Ход урока:
Задание 1
Переведи двоичное число 1101001112 в восьмеричную систему счисления.
Решение:
Разобьем двоичное число на триады и по таблице оснований систем счисления переведем число в восьмеричную систему счисления. Получим:
1101001112=6478.
Ответ: 6478.
Задание 2
Переведи восьмеричное число 3568 в двоичную систему счисления.
Решение.
Переведем восьмеричное число 3568 в двоичную систему счисления, используя таблицу оснований системы счисления. Уберем слева один незначащий 0. Получим:
3568=0111011102=111011102.
Ответ: 111011102.
Задание 3
Среди приведенных ниже трех чисел, записанных в различных системах счисления, найди наименьшее и запиши его в ответе в десятичной системе счисления.
1111012, 768, 2816
Решение.
Переведем все три числа в десятичную систему счисления.
5 4 3 2 1 0
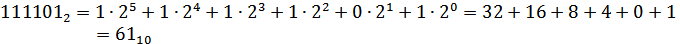
1 0
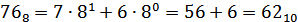
1 0
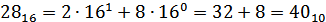
Наименьшее число 2816=4010.
Ответ: 4010.
Изучение нового материала.
Новый материал изучи в сопровождении презентации. Прежде всего необходимо просмотреть обучающее видео.
Запиши в тетради таблицу степеней чисел 8 и 16.
| n | 8n | 16n |
| 0 | 1 | 1 |
| 1 | 8 | 16 |
| 2 | 64 | 256 |
| 3 | 512 | 4096 |
| 4 | 4096 | 65536 |
| 5 | 32768 | 1048576 |
Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15).
2 1 0
3АF16 =3*162+10*161+15*160 =768+160+15=94310.
Запиши в тетрадь
Переведём десятичное число 154 в шестнадцатеричную систему счисления:
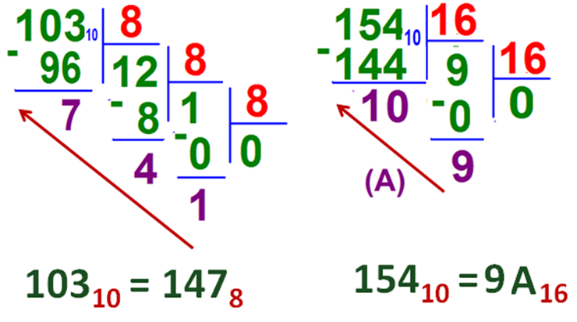
Правило перевода целых десятичных чисел в систему счисления с основанием q
1. последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
2. полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3. составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
3. Решим задачи в тетради:
№ 51 (РТ) Слайд 12
Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
25610, 40010, 123410, 201210,
Запиши в тетрадь!!!!
Не торопись, вдумчиво читай задания. Внимательно читай требования к тому, в каком виде представить ответ. Разрешается использовать калькулятор.
Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найди наибольшее и запиши его в ответе в десятичной системе счисления.
1110102, 658, 3616
Проверь себя! Решение. Переведем все три числа в десятичную систему счисления.
5 4 3 2 1 0
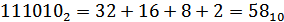
1 0
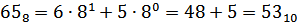
1 0
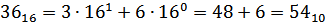
Наибольшее число 3616=5410.
Ответ: 5410.
Задание 2.
Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найди наибольшее и запиши его в десятичной системе счисления.
1100102, 678, 3С16
Проверь себя! Решение. Переведем все три числа в десятичную систему счисления.
5 4 3 2 1 0
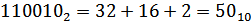
1 0
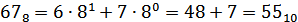
1 0
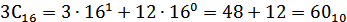
Наибольшее число 3С16=6010.
Ответ: 6010.
Домашнее задание. § 1.1 (п.1.1.4, 1.1.5, 1.1.7) выучить, ответить устно на вопросы № 1-5 (с.14)








