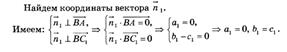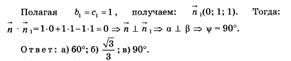Косинус угла между плоскостями равен модулю косинуса угла между векторами нормалей к этим плоскостям.
Пусть плоскость 
задается точками 
, а плоскость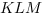 
точками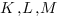 
2.1. Находим координаты точек .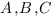
2.2. Находим уравнение плоскости .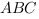
Для этого координаты точек 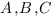подставляем в уравнение плоскости : 
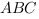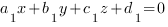. Получим систему из трех уравнений с тремя неизвестными. Решая ее, находим коэффициенты 
.
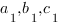Коэффициенты 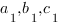в уравнении плоскости являются координатами вектора нормали к плоскости : 
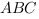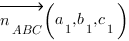
2.3. Находим координаты точек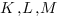
2.4. Находим уравнение плоскости 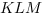. Для этого координаты точек 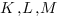подставляем в уравнение плоскости : 
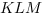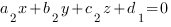
Получаем систему из трех уравнений с тремя неизвестными. Решая ее, находим коэффициенты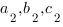 
.
Коэффициенты 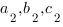в уравнении плоскости являются координатами вектора нормали к плоскости : 
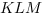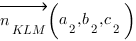
Косинус угла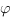 
между плоскостями находится по такой формуле:
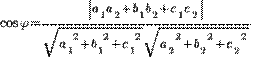
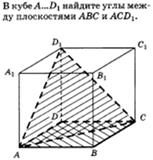
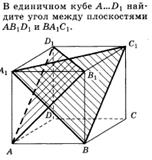
Примеры:
2.1 2.2
3. Угол между прямой и плоскостью.
Зная координаты направляющего вектора прямой и вектора нормали к плоскости, мы можем найти косинус угла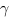 
- угла между вектором нормали к плоскости. Но нам нужен угол 
. 
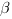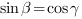
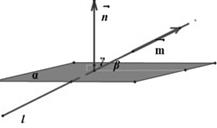
Пусть нам нужно найти угол между прямой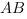 
, проходящей через точки 
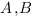и плоскостью 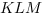, проходящей через точки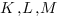
3.1. Находим координаты точек .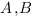
3.2. Находим координаты вектора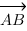 
: 
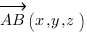
3.3. Находим координаты точек .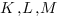
3.4. Находим уравнение плоскости 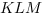. Для этого координаты точек 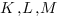подставляем в уравнение плоскости : 
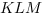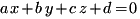
Получаем систему из трех уравнений с тремя неизвестными. Решая ее, находим коэффициенты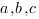 
.
Коэффициенты 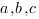в уравнении плоскости являются координатами вектора нормали к плоскости : 
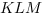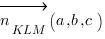Косинус угла 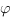между вектором нормали к плоскости 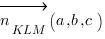и направляющим вектором прямой 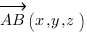равен
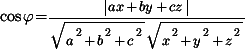
Синус угла между прямой 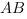и плоскостью 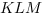равен косинусу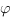
Примеры:
3.1 3.2
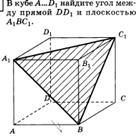
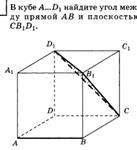
Три типа задач на нахождение расстояний в пространстве.
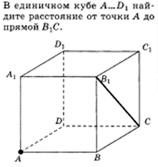
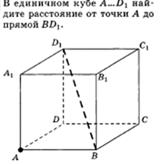
1. Расстояние от точки до плоскости.
Рассстояние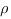 
от точки 
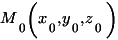до плоскости 
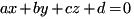вычисляется по такой формуле:
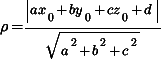
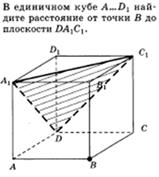
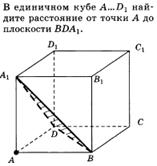
Примеры:
1.1 1.2
2. Расстояние между скрещивающимися прямыми
Пусть нужно найти расстояние между прямым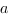и 
и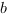 
:
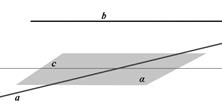
2.1Проводим через любую точку прямой 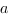прямую 
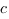параллельную прямой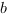
2.2 Прямые 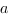и 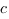задают плоскость 
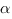, которая параллельна прямой .
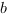2.3. Находим расстояние от любой точки прямой 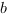до плоскости .
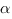Оно равно расстоянию между прямым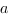и и .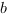
Чтобы найти уравнение плоскости 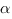, берем три точки, одна из которых принадлежит прямой 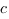, а две другие прямой .
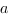Пример:
2.1 2.2
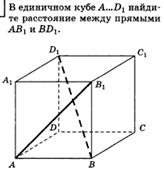
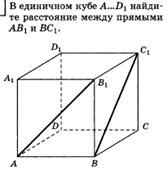
3. Расстояние от точки до прямой.
Пусть нам надо найти расстояние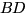 
от точки 
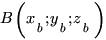до прямой 
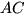, которая определяется точкам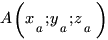и 
и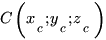 
:
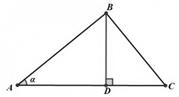
3.1. Находим координаты вектора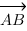
3.2. Находим координаты вектора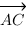 
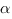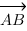3.3. Находим косинус угла между и .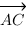
3.4. Находим синус угла 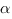с помощью основного тригонометрического тождества.
3.5. Находим длину вектора :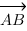 
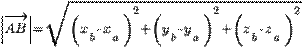
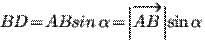
Примеры:
3.1 3.2
