Метод координат в решении задач стереометрии.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
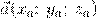
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
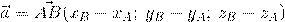
Длина или модуль вектора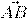 
в пространстве – это расстояние между точками A и B.
Находится как корень квадратный из суммы квадратов координат вектора.
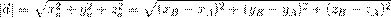
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
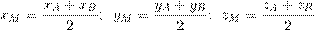
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы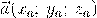 
и 
.
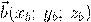Сумма векторов:
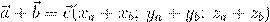
Разность векторов:
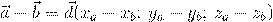
Произведение вектора на число:
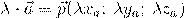
Скалярное произведение векторов:
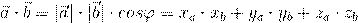
Нахождение косинуса, а, следовательно, и самого угла, между двумя векторами с заданными координатами осуществляется по формуле:
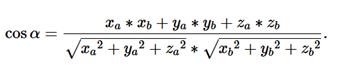
Для решения задач необходимо научиться находить координаты вершин основных многогранников при помещении их в прямоугольную систему координат.
Ниже представлены координаты вершин некоторых многогранников, помещенных в систему координат.
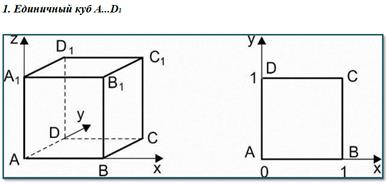
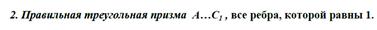
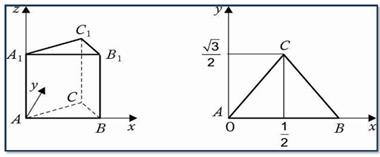
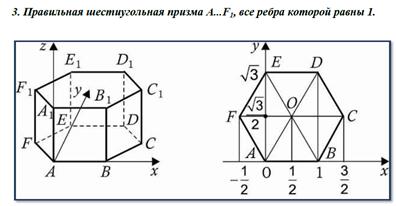
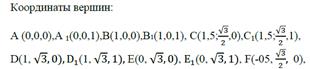
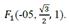
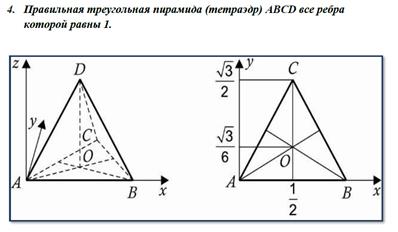
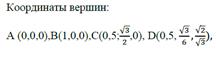
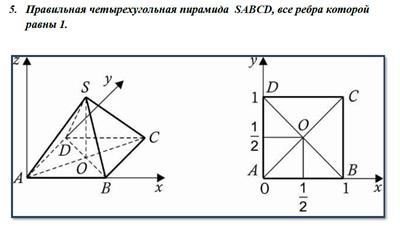
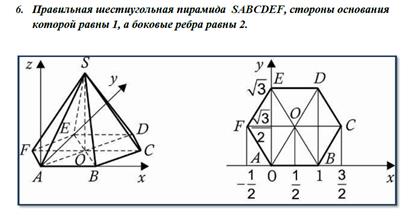
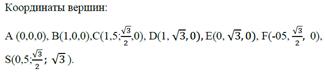
Три типа задач на нахождение углов в пространстве.
1.Угол между прямым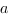и 
и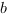 
.
Величиной угла между прямыми называется величина меньшего из углов, образованных этими прямыми.
Косинус угла между прямыми равен модулю косинуса угла между направляющими векторами этих прямых.
Пусть прямая 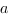проходит через точк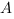и 
и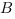 
, а прямая 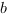через точк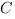и 
и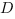 
1.1 Находим координаты точек 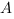и 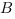, затем находим координаты вектора 
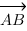. Для этого из координат точки 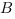вычитаем координаты точки .
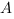Вектор 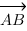- направляющий вектор прямой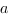
1.2. Находим координаты точек 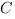и 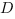, затем находим координаты вектора 
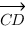. Для этого из координат точки 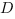вычитаем координаты точки .
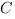Вектор 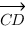- направляющий вектор прямой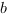
1.3. Итак:
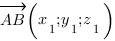и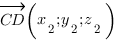 
.
Тогда:
Косинус угла между прямыми вычисляется по формуле:
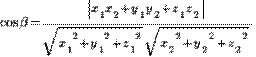
Примеры:
1.1 1.2
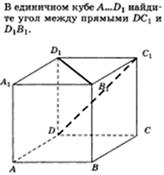
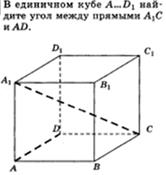
2. Угол между плоскостями.