Дискретизация системы методом конечных разностей

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Для отыскания численного решения для поля температур проведем дискретизацию системы следующим образом (рисунок 3):

1) Рассмотрим теплопроводящую среду как ряд точек (узлов). Для этих точек отыскиваются значения температуры, а для всех остальных точек среды значения температур интерполируются по значениям в соседних узловых точках.

2) Масса и соответствующая ей теплоемкость среды сосредотачиваются в ближайших узлах.

3) Узлы, между которыми в соответствии с геометрической и физической конфигурацией среды возможна теплопроводность, соединяются связями. Эти связи характеризуются эффективными длинами путей передачи тепла и эффективными площадями поперечного сечения материала на этих путях, а также коэффициентами теплопроводности.

Таким образом, свойства среды по накоплению тепла учитываются в свойствах узлов, а свойства теплопроводности в свойствах связей между узлами.

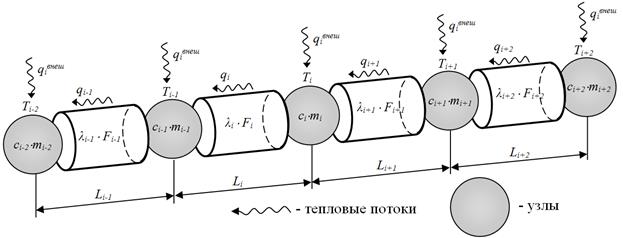
Рисунок 3 – Дискретизация в задаче теплопередачи в стержне

Тогда уравнение теплового баланса для i-ого узла примет вид:

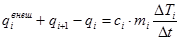, (9)

Где Dt – шаг интегрирования по времени, q_i^внеш – внешний тепловой поток, приходящийся на i-ый узел, а DT_i – изменение температуры i-ого узла за время Dt. Подставляя (2) в (9) получим:

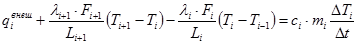. (10)

Представляя DT_i как разность температур для соседних шагов по времени (DT_iⁿ = T_iⁿ - T_i^n-1) и группируя члены с Ti, перепишем (10) в виде:

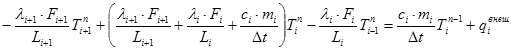. (11)

Зная поле температур на предыдущем шаге по времени, можно решить систему таких уравнений теплового баланса для всех узлов системы относительно температур на новом шаге по времени.

Дискретизация в задаче с теплопроводностью в пространстве будет отличаться от одномерной задачи следующим:

¾ узлы будут располагаться на вдоль одной линии, а в трехмерном пространстве;

¾ связей между узлами будет больше и, следовательно, в каждом уравнении теплового баланса будут участвовать не три, а семь узлов (смотри уравнение 8).

Объединяя уравнения (11) для всех узлов получим систему:

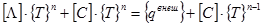, (12)
где {T}ⁿ - вектор узловых температур в n-ый момент времени, [C] – матрица теплоемкости (диагональная матрица с коэффициентами C_ii = c_i × m_i /Dt) [ L] – матрица теплопроводности. Ее коэффициенты равны множителям из уравнений (11) при Т, содержащие λ_i+1 и λ_i . На каждом шаге интегрирования во времени решаем это уравнение относительно {T}ⁿ . Найденное ранее решение с предыдущего шага является {T}^n-1 .

Численное решение для установившейся теплопередачи в одномерном проводнике тепла

Рассмотрим систему, состоящую из трех последовательно соединенных стержней (рисунок 4). Стержни имеют одинаковые длины, L, и площади поперечных сечений, F. Стержни сделаны из одного материала с теплопроводностью λ. Левый конец стержня свободный, а правый присоединен к термостату с температурой T`. К одной из средних точек подходит постоянный по времени поток тепла, q^внеш .

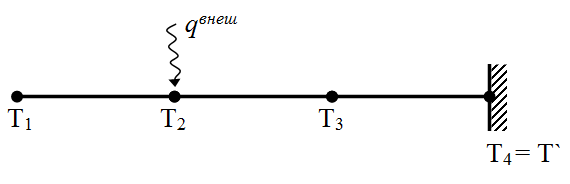
Рисунок 4 – Модель одномерного проводника тепла с четырьмя узлами

С течением времени в этой системе установится постоянное по времени поле температур. Требуется найти это поле. Подставляя в (11) T_i^n-1 = T_iⁿ (температура не меняется во времени) и учитывая, что λ_i = λ;×F_i = F; L_i = L, получим:

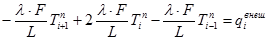. (13)

В рассматриваемой системе есть три неизвестные температуры – в узлах 1, 2 и 3. Для нахождения их значений нужно составить линейную систему из трех уравнений. Можно составить уравнение (13) для i = 2 и 3. Для i = 1 составлять такое уравнение не получается поскольку для него нет T_i-1 . Поскольку узел 1 лежит на левом конце проводника тепла, тепловой поток в левую сторону из этого узла равен нулю. Если бы слева от узла 1 было бы продолжение проводника тепла с узлом 0, то тогда тепловой поток от узла 1 к узлу 0 был бы равен нулю если бы температуры этих узлов были бы равны: T₁ = T₀ . При введении узла 0 в систему появляется возможность составить уравнение (13) для узла 1. Введем узел 0 в систему и она примет вид, показанный на рисунке 5.

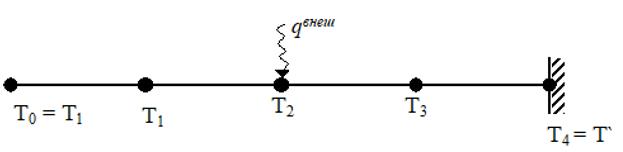
Рисунок 5 – Модель одномерного проводника тепла с дополнительным узлом для отображения отсутствия теплового потока через свободный край

С учетом вышесказанного уравнения (13) для узлов 1, 2 и 3 запишутся в виде:

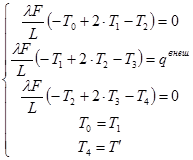. (14)

Умножив четвертое и пятое уравнения системы (14) на l×F/L и переписав ее в матричной форме получаем:

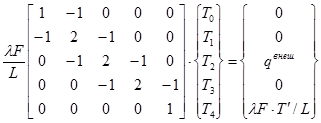. (15)

Первое уравнение (15) выражает Т0 через Т1, а поскольку значение Т0 нам не нужно, то это уравнение можно выбросить. Значение Т4 из пятого уравнения подставляем в четвертое и член содержащий Т` переносим в правую часть. После этого (15) примет вид:

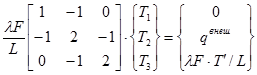(16)

Решаем систему (16) методом Гаусса и получаем решение: Т₁ = T₂ = 2×q^внеш×L/(l×F)+T¢ ; T₃ = q^внеш×L/(l×F)+T¢ . Это решение показано на рисунке 6.

Получилось, что тепло приходит в узел 2. Благодаря перепаду температур это тепло перетекает на термостат (узел 4). В сторону узла 1 тепло не идет, поскольку перепада температуры между узлами 1 и 2 нет. Это логично, поскольку теплу с узла один некуда идти кроме как назад на узел 2. Если какое-то количество тепла перешло бы с узла 2 на узел 1, то температура узла 1 поднялась бы. Появился бы перепад температур, обуславливающий обратный переток тепла с узла 1 на узел 2 . Этот переток продолжался бы до тех пор, пока температуры этих узлов снова не стали бы равны. Видим, что найденное решение интуитивно понятно и не видно каких-либо нелогичностей, свидетельствующих об ошибке.

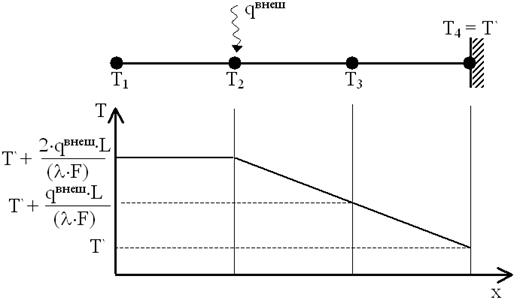
Рисунок 6 – Распределение температур по длине линейного проводника тепла

Дискретизация в задаче теплопроводности в сплошной трехмерной среде принципиально не отличается от рассмотренной. Соотношения будут более громоздкими и менее наглядными. Поэтому рассматривать здесь ее не будем.

Итак, мы рассмотрели дискретизацию в задаче теплопроводности и на простом примере разобрали, какие вычисления выполняет система автоматизированного проектирования при решении этой задачи численными методами.