Решение задачи теплопередачи методом конечных разностей
Вспомним основные соотношения, определяющие процесс теплопередачи в материале. Тепло – это энергия движения частиц материи. В газе или в жидкости это энергия броуновского движения молекул, в твердом теле – энергия колебания атомов. Мерой кинетической энергии этого движения является температура. Если есть некоторое количество материала, то для увеличения кинетической энергии его частиц нужно сообщить материалу тепловую энергию – некоторое количество тепла Q. Изменение температуры D T связано с сообщенным материалу количеством тепла соотношением:
Q = c × m × D T, (1)
где c – теплоемкость материала, m – масса нагреваемого материала.
Тепло распространяется по материалу от более нагретой части к менее нагретой части – температура материала со временем выравнивается по всему объему. Скорость перетекания тепла (тепловой поток) между частями тела со значениями температуры Т1 и Т2 равна:
q = dQ/ dt = λ × F ×( Т1 - Т2)/ L, (2)
где λ – коэффициент теплопроводности материала, F – площадь поперечного сечения материала через которую передается тепло (рис. 1), L – длина пути передачи тепла.
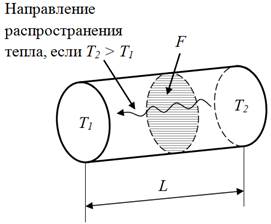
Рисунок 1 – Теплопроводность в теле простой геометрической формы
В общем случае и теплопроводность, и площадь поперечного сечения могут меняться по объему тела. Рассмотрим одномерный проводник тепла (рисунок 1). Координату x будем откладывать вдоль этого проводника. Рассмотрим его участок с бесконечно малой длиной dx и перепадом температуры dT. Тогда скорость перетока тепла через этот участок составит
q=λ(x)×F(x) dT/dx . (3)
Скорость притока дополнительного тепла к этому участку будет равна разнице притока тепла с одной стороны и оттока тепла в другую сторону. Эта разница равна изменению теплового потока между концами участка, а именно производной теплового потока по длине проводника тепла перемноженной на длину участка (в случае элементарного участка - dx) – dq/dx×dx. Кроме того нужно прибавить внешний тепловой поток к этому участку
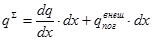 . (4)
. (4)
где qпогвнеш – погонный внешний тепловой поток (на единицу длины проводника тепла).
Скорость притока дополнительного тепла приведет к увеличению температуры на этом участке со скоростью dT/dt. Эта скорость связана со скоростью притока тепла в соответствии с (1) так:
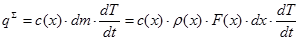 , (5)
, (5)
где r - плотность материала. Подставляя (3) и (4) в (5) получим:
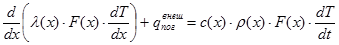 . (6)
. (6)
Рассмотрим теплопроводность в сплошной однородной среде. В среде есть переменное поле температуры T(x,y,z). В любой точке среды вектор градиент температуры ÑT направлен в сторону наибыстрейшего увеличения температуры. В направлениях перпендикулярных градиенту температуры температура не изменяется. Поскольку теплопроводность происходит только при перепаде температуры, делаем вывод, что теплопередача в любой точке однородной среды будет происходить в одном направлении – в направлении противоположном градиенту температуры. Теплопроводность в сплошной однородной среде подобна теплопроводности в одномерном проводнике тепла с постоянными характеристиками материала по длине и постоянной площадью поперечного сечения. Тогда если взять систему координат, ось x которой совпадает с ÑT, то уравнение (6) перепишется для сплошной среды в виде:
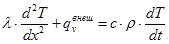 , (7)
, (7)
где qvвнеш – внешний тепловой поток на единицу объема: qvвнеш = qпогвнеш/F.
При получении (7) учли, что теплопроводность, теплоемкость и плотность материала не зависят от координаты. Площадь поперечного сечения одномерного проводника тепла заменяется на площадь элементарного участка сечения материала, перпендикулярного ÑT – dF . Площадь элементарного участка dF при получении (7) сокращается. Предположим, ÑT имеет все три компоненты: ÑT = (dT/dx, dT/dy, dT/dz). Выражение (7) означает, что тепловой поток, идущий на нагревание материала элементарного объема, складывается из внешнего теплового потока и разницы тепловых потоков на противоположных сторонах объема. При несовпадении оси X системы координат с ÑT, проходящий через элементарный объем тепловой поток рассматривается как три тепловых потока по направлениям X, Y, и Z. Тогда тепло на нагревание материала элементарного объема складывается из внешнего теплового потока и разницы этих трех тепловых потоков на противоположных сторонах объема (рисунок ).
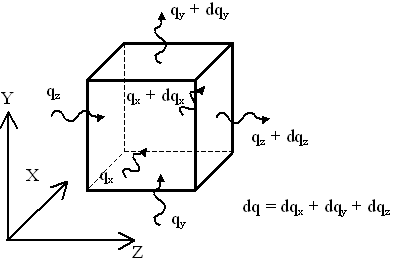
Рисунок 2 – Нагревающее элементарный объем тепло при теплопередаче в трехмерной среде
С учетом этого (7) перепишется в виде:
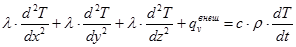 (8)
(8)
Так выглядит дифференциальное уравнение, описывающее теплопроводность в сплошной среде. Во внешний тепловой поток входит как внешний по отношению к системе нагрев, так и тепло переносимое конвекцией и радиацией. Для того чтобы воспользоваться преимуществами численных методов при моделировании теплопроводности нужно провести дискретизацию сплошной среды, что и будет сделано далее.








