Тема урока: Решение задач по теме:«Энергия связи. Дефект масс».
05.04.2023 Физика 9
Тема урока: Решение задач по теме:«Энергия связи. Дефект масс».
Цель урока : научить решать задачи на расчет дефекта масс, энергии связи атомных ядер.
Ход урока.
I. Организационный момент
II. Проверка знаний
1. Что называется энергией связи ядра?
Ответ: Минимальная энергия, необходимая для расщепления ядра на отдельные нуклоны, называется энергией связи ядра.
2. Запишите формулу для определения дефекта массы ядра любого атома.
Ответ:
 , где
, где 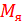 - масса ядра атома, Z – число протонов, N – число нейтронов,
- масса ядра атома, Z – число протонов, N – число нейтронов, 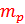 - масса протона,
- масса протона, 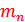 - масса нейтрона. Масса ядра всегда меньше суммы масс нуклонов, из которых оно состоит.
- масса нейтрона. Масса ядра всегда меньше суммы масс нуклонов, из которых оно состоит.
Разность между суммы масс нуклонов и массы ядра называется дефектом масс.
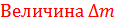 называет дефектом масс.
называет дефектом масс.
2. Запишите формулу для расчета энергии связи ядра атома.
Ответ: 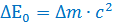 , где с =
, где с = 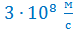 - скорость света в вакууме.
- скорость света в вакууме.
III. Решение задач
В ядерной физике массу принято выражать в атомных единицах массы (а.е.м.).
А.е.м. равна 1/12 массы нуклида углерода 12С, что в единицах СИ составляет 1,660565 • 10 - 27 кг.
Масса покоя электрона равна 5,4858 ∙ 10 – 4 а.е.м. = 9,1∙10 -31кг
Масса покоя протона 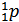 равна 1,00728 а.е.м. =1,6726∙10-27 кг
равна 1,00728 а.е.м. =1,6726∙10-27 кг
Масса покоя нейтрона 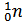 равна 1,00866 а.е.м. =1,6749∙10-27 кг
равна 1,00866 а.е.м. =1,6749∙10-27 кг
Масса покоя водорода 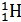 равна 1,00783 а.е.м.
равна 1,00783 а.е.м.
Масса покоя дейтерия 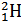 равна 2,01410 а.е.м.
равна 2,01410 а.е.м.
Масса покоя гелия 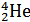 равна 4,00260 а.е.м.
равна 4,00260 а.е.м.
с2 = 931,5 МэВ/ а.е.м., где с — скорость света.
Масса электрона мы пренебрегаем при решении задач.
те  тр
тр
Образец решения задачи.
Задачи. Вычислите энергию связи  Е0 ядра гелия
Е0 ядра гелия 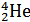 .
.
Решение. Масса атома гелия: 4,00260 а.е.м. Z=2, N =2
Масса отдельных (невзаимодействующих между собой) нуклонов:
| + |
2∙ тр = 2 ∙1,00728 а.е.м.= 2,01456 а.е.м.
2∙тп = 2 ∙1,00866 а.е.м. = 2,01732 а.е.м.
4,03188 а.е.м.
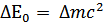
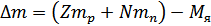
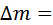 4,03188 а.е.м. - 4,00260 а.е.м. = 0,02928 а.е.м.
4,03188 а.е.м. - 4,00260 а.е.м. = 0,02928 а.е.м.
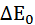 = 0,02928 а.е.м. • 931,5 МэВ/ а.е.м. = 27,27432 МэВ
= 0,02928 а.е.м. • 931,5 МэВ/ а.е.м. = 27,27432 МэВ
Ответ: энергия связи 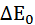 ядра гелия
ядра гелия 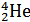 ≈27,3 МэВ.
≈27,3 МэВ.
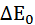 ≈ 27,3 МэВ или
≈ 27,3 МэВ или 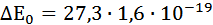 Дж =43,68
Дж =43,68 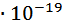 Дж.
Дж.
Решите задачи.
Задача 1. Вычислите энергию связи  E 0 ядра гелия
E 0 ядра гелия 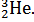
Решение:
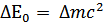
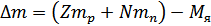
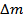 =3,02322 а.е.м. – 3,01602а.е.м. = 0,0072 а.е.м. =3,02322 а.е.м. – 3,01602а.е.м. = 0,0072 а.е.м.
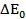 = 0,0072 а.е.м. ∙ 931,5 МэВ/ а.е.м. =6,7068 МэВ
Ответ: = 0,0072 а.е.м. ∙ 931,5 МэВ/ а.е.м. =6,7068 МэВ
Ответ:  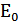 ≈ 6,71 МэВ ≈ 6,71 МэВ
|
1.Дано:
Мя ( 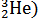 = 3,01602 а.е.м.
= 3,01602 а.е.м.
Z = 2; N =1
2∙ тр = 2 ∙1,00728 а.е.м.= 2,01456 а.е.м.
1∙тп = 1∙ 1,00866 а.е.м. =1,00866 а.е.м.
 E 0 =?
E 0 =?
Задача 2. Вычислите энергию связи  E 0 ядра трития
E 0 ядра трития 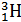 .
.
Решение:
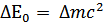
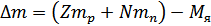
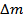 =(1,00728+2,01732) а.е.м.– =(1,00728+2,01732) а.е.м.– 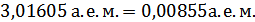
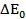 = 0,00855 а.е.м. ∙ 931,5 МэВ/ а.е.м. =7,964325 МэВ
Ответ: = 0,00855 а.е.м. ∙ 931,5 МэВ/ а.е.м. =7,964325 МэВ
Ответ: 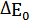 ≈ 7,96 МэВ ≈ 7,96 МэВ
|
Дано:
Мя( 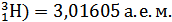
Z = 1; N =2
1∙ тр = 1 ∙1,00728 а.е.м.= 1,00728 а.е.м.
2∙тп = 2∙ 1,00866 а.е.м. =2,01732 а.е.м.
 E 0 =?
E 0 =?
Задача 3. Вычислите энергию связи ядра лития 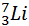 .,
.,
Дано:
Мя ( 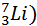 =7,01601 а.е.м.
=7,01601 а.е.м.
Решение:
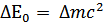
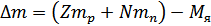
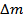 =(3,02184+4,03464) а.е.м.– =(3,02184+4,03464) а.е.м.– 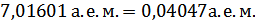
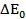 = 0,04047 а.е.м. ∙ 931,5 МэВ/ а.е.м. =37,697805 МэВ
Ответ: = 0,04047 а.е.м. ∙ 931,5 МэВ/ а.е.м. =37,697805 МэВ
Ответ: 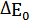 ≈ 37,70 МэВ ≈ 37,70 МэВ
|

Z = 3; N =4
3∙ тр = 3 ∙1,00728 а.е.м.= 3,02184 а.е.м.
4∙тп = 4∙ 1,00866 а.е.м. =4,03464 а.е.м.
 E 0 =?
E 0 =?
Задача 4
Рассчитайте дефект массы и энергию связи ядра атома кислорода 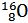 .
.
Решение:
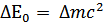
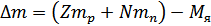
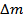 =(8,05824+8,06928) а.е.м.– =(8,05824+8,06928) а.е.м.– 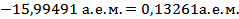 =
= 0,13261∙1,66 =
= 0,13261∙1,66 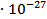 кг ≈2,2 кг ≈2,2 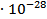 кг кг
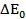 =0,13261 а.е.м. ∙ 931,5 МэВ/ а.е.м. ≈123,53 МэВ =123,53∙1,6 =0,13261 а.е.м. ∙ 931,5 МэВ/ а.е.м. ≈123,53 МэВ =123,53∙1,6 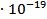 Дж= 197,64 Дж= 197,64 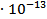 Дж
Ответ: Дж
Ответ: 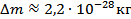 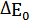 ≈ 197,64 ≈ 197,64 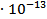 Дж ≈1,98 Дж ≈1,98 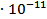 Дж Дж
|
Дано:
Мя ( 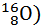 =15,99491 а.е.м.
=15,99491 а.е.м. 
Z = 8; N =8
8∙ тр = 8 ∙1,00728 а.е.м.= 8,05824 а.е.м.
8∙тп = 8∙ 1,00866 а.е.м. = 8,06928 а.е.м.
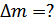
 E 0 =?
E 0 =?
Домашнее задание. § 60-62.
Задача 1. Определите дефект масс ядра атома бора 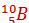 в атомных единицах массы и килограммах. Мя (
в атомных единицах массы и килограммах. Мя ( 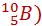 =10,01294 а.е.м
=10,01294 а.е.м
Задача2. Вычислите энергию связи ядра лития 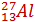
Мя ( 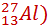 =26,98153 а.е.м
=26,98153 а.е.м








