Определение усилий в диссипативных системах.
Определить усилия в диссипативной системе на рис. 6 от заданных возмущений. Коэффициенты внутреннего трения в первом, втором и третьем элементах 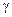 =0.02. Влиянием внутреннего трения остальных элементов пренебрегаем.
=0.02. Влиянием внутреннего трения остальных элементов пренебрегаем.
В расчетах диссипативных систем M1(12) = 7. Компоненты седьмых столбцов матриц EI равны коэффициентам внутреннего трения.
Остальные компоненты указанных матриц равны фактическим значениям соответствующих величин.
Матрицы LI составляются так же, как и в расчетах без учета внутреннего трения.
P1 = 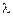
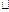 EJ
EJ 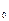 ,
, 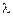 = k/EA, R1 = N/EJ
= k/EA, R1 = N/EJ 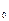
С учетом сказанного матрицы M1, E1, E2, E3 и E4 имеют вид:
E1= 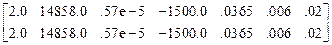 ,
,
E2= 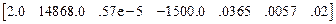 ,
,
E3= 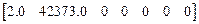 ,
,
E4= 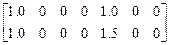 .
.
Основные неизвестные определятся из уравнения:

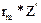 (t) +
(t) + 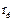
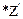 (t) +
(t) + 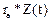 +
+ 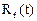 = 0,
= 0,
от гармонических возмущений в моменты времени : ( 0, .707, 1.00, .707, 0 )*Т , (Т = 0,5* 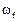 ,
, 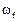 =53.0 р/с);
=53.0 р/с);
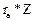 +
+ 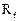 = 0
= 0
от статических возмущений.
Усилия в заданные моменты времени в элементах заданной системы определяются по формуле (18) первой части пособия. Они образуют матрицы:
r 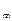 =
= 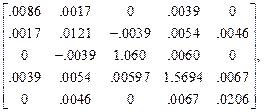
r 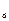 =
= 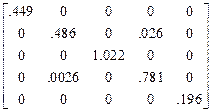 ,
,
r 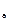 =
= 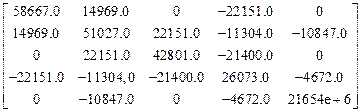 ,
,
R 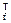 =
= 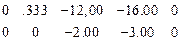
.Матрица Z обобщенных координат равна матрице:
Z= 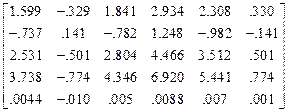 *10
*10 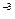 .
.
Матрица Z  первых производных
первых производных
Z 
 =
= 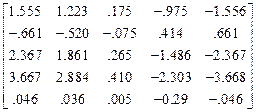 *10
*10 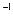 ,
,
Матрица Z 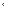 вторых производных
вторых производных
Z  =
= 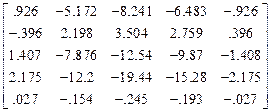 .
.
Матрицы усилий в элементах заданной системы :
Первый элемент
M  ; -32.45 6.17 -34.56 -55.05 -43.28 -6.17
; -32.45 6.17 -34.56 -55.05 -43.28 -6.17
Q  ; 19.73 -3.42 19.24 30.63 24.08 3.42
; 19.73 -3.42 19.24 30.63 24.08 3.42
Q 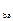 ;17.73-3.2219.1430.2923.693..22
;17.73-3.2219.1430.2923.693..22
M 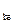 ; -8.81 1.52 -7.97 -12.79 -10.12 -1.52
; -8.81 1.52 -7.97 -12.79 -10.12 -1.52
Второй элемент
M 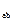 ; 8.81 -1.51 7.97 12.79 10.12 1.52
; 8.81 -1.51 7.97 12.79 10.12 1.52
Q 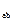 ; 7.73 - 1.81 9.85 15.74 12.42 1.8
; 7.73 - 1.81 9.85 15.74 12.42 1.8
Q 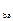 ;5.73 -1,41 9.23 14.46 11.22 1.41
;5.73 -1,41 9.23 14.46 11.22 1.41
M 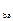 ; -24.09 5. 31 -29.33 -46.80 -36.85 -5.31
; -24.09 5. 31 -29.33 -46.80 -36.85 -5.31
Третий элемент
M 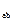 ; 24.09 -5.31 29.34 46.80 36.85 5.31
; 24.09 -5.31 29.34 46.80 36.85 5.31
Q 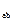 ; -9,27 1.84 -11.22 -17.70 -13.811.83
; -9,27 1.84 -11.22 -17.70 -13.811.83
Q 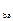 ; -9.27 2.05 -11.64 -18.51 -14.54 -2.0
; -9.27 2.05 -11.64 -18.51 -14.54 -2.0
Четвертый элемент
N 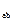 ;-9.27 2.06 -11.64 -18.51 -14.54 2.06
;-9.27 2.06 -11.64 -18.51 -14.54 2.06
N 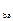 ; -9.26 2.06 -11.64 -18.51 -14.54 -2.06
; -9.26 2.06 -11.64 -18.51 -14.54 -2.06
Пятый элемент
-F; 10.00 -1.41 9,29 14.54 11.28 1.41
Шестой элемент
-F; 15.00 -3.26 20.43 32.16 25.05 3.26
Компоненты первых столбцов–усилия от статических возмущений, вторых, третьих, четвертых, пятых и шестых – от заданных динамических возмущений в моменты времени : 0*T, .125*T, .25*T, .375*T, .5*T (T=55.789 р/сек – период собствен-ных колебаний.
3. Тонкие плиты
Структурная и количественная характеристики системы определяются матрицей – строкой M1. В расчетах методом конечных элементов в форме метода перемещений M1(1) = M1(2) = M1(0) = M1(10) = M1(11) = 0. М1(3) = число основных неизвестных, М1(4) =2 (признак метода перемещений), М1(5) – число тонкостенных стержней в состоянии стесненного кручения; М1(6), М1(7), М1(8), М1(9) - число элементов первого, второго, третьего и четвертого типов; М1(17), М1(18), М1(19), М1(20) - число элементов пятого, шестого, седьмого и восьмого типов. М1(12) - в расчетах на статические возмущения =1, в расчетах на устойчивость = 2, в расчетах на статические и гармонические возмущения = 5, в расчетах на мгновенный импульс = (-3), в расчетах на динамические возмущения, изменяющиеся во времени по произвольному закону =6, в расчетах диссипативных систем =7. М1(13) - число линейно независимых возмущений, М1(14) - число сочетаний заданных возмущений, М1(16) - число статических возмущений. М1(15) =0, если осуществляется оптимизация конструкции М1(15)>0.
3.1. Основная система. Исходные данные
Рассчитываемая плита разбивается на прямоугольные и треугольные элементы. Предпочтение следует отдать разделению только на прямоугольные элементы. За основные неизвестные принимаются угловые и линейные перемещения узлов. Положительные линейные перемещения – перемещения в направлении положительной оси Z; положительные угловые перемещения – повороты по часовой стрелке относительно оси Y (dw/dx) и повороты против часовой стрелки относительно X (dw/dy), если смотреть в начало координат.
В матрицах 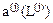 - матрицах перемещений узлов, соответствующих единичным значениям основных неизвестных, компоненты первой строки – углы поворота узла i относительно
- матрицах перемещений узлов, соответствующих единичным значениям основных неизвестных, компоненты первой строки – углы поворота узла i относительно
оси Y, компоненты второй – его линейные перемещения, компоненты третьей – углы поворота относительно оси X. Затем в той же последовательности вводятся перемещения узлов j, k, l. Для треугольных элементов – компоненты десятой строки – угловые перемещения среднего сечения гипотенузы. Число столбцов в матрицах 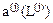 равно числу основных неизвестных плюс число линейно независимых заданных возмущений. Заданные возмущения заменяются узловыми возмущениями, действующими на элементы четвертого типа. Поэтому компоненты n+1, n+2,…, n+m столбцов матриц
равно числу основных неизвестных плюс число линейно независимых заданных возмущений. Заданные возмущения заменяются узловыми возмущениями, действующими на элементы четвертого типа. Поэтому компоненты n+1, n+2,…, n+m столбцов матриц 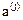 равны нулям (m – число заданных возмущений). Порядок нумерации основных неизвестных может быть произвольным.
равны нулям (m – число заданных возмущений). Порядок нумерации основных неизвестных может быть произвольным.
На печать выдаются изгибающие моменты в узловых точках, изгибающие и крутящие моменты в центре элемента.В системах, расчетная схема которых состоит из сравнительно большого числа элементов, за расчетные усилия принимаются изгибающие и крутящие моменты в центрах элементов. В остальных - изгибающие моменты в узлах. Они определяются в виде суммы усилий в примыкающих к узлу элементов, поделенной на число указанных элементов.
Упругие характеристики элементов основной системы задаются величинами: D 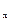 =E
=E 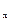 *h
*h 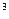 / (12*
/ (12* 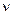 ), D
), D 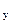 =E
=E 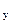 *h
*h 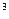 /(12*
/(12* 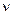 ), D
), D 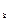 =G*h
=G*h 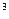 /6, D
/6, D 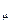 =
= 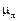 *D
*D 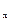 =
= 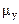 D
D 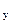 ,
, 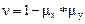 . М - интенсивность массы, М
. М - интенсивность массы, М 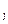 - интенсивность момента инерции массы.
- интенсивность момента инерции массы.
Геометрические и упругие характеристики элементов основной системы образуют прямоугольные матрицы EI вида
EI= [ 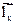
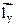
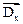
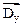
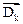
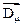
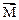
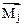
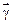 ].
].
Число строк равно числу элементов данного типа. В статических задачах векторы M масс, моментов инерции M 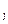 масс, и коэффициентов
масс, и коэффициентов 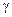 внутреннего трения и демпфирования не вводятся.
внутреннего трения и демпфирования не вводятся.
3.2. Расчет тонкой плиты
на статические и гармонические возмущ ения
В защемленной по контуру железобетонной плите (рис.14) определить усилия от статических нагрузок 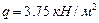 ,
, 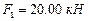 и амплитудные значения усилий от гармонической нагрузи F(t)
и амплитудные значения усилий от гармонической нагрузи F(t) 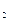 =1.0*Sin(148*t) kH, приложенных в центре плиты.
=1.0*Sin(148*t) kH, приложенных в центре плиты.
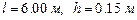 .
. 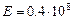
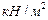 ,
, 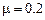 ,
,
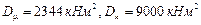 .
.
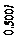
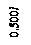
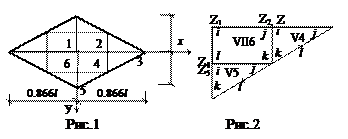
Рис.14 Рис.15
Учитывая симметрию, усилия определим в четверти заданной системы (рис.15). Выделенную часть в расчете представим шестью элементами. Узлы 1, 2, 6 с сосредоточенными силами – элементы четвертого типа с порядковыми номерами 1, 2, 3. Треугольники 234,456 (рис.14)– элементы пятого типа с порядковыми номерами V4, V5 (рис.15). Прямоугольный элемент 1246 –элемент седьмого типа, порядковый номер VII-6.
На первый элемент действует статическая сила 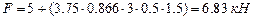 и динамическая - с амп-
и динамическая - с амп-
литудным значением 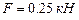 . На второй и третий статические силы
. На второй и третий статические силы 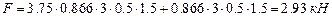 .
.
Исходные данные:
M1 = [ 0 0 5 2 0 0 0 0 3 0 0 5 2 0 0 1 2 0 1 0 ]
E4 = 
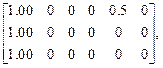
Lx Ly Dx Dy Dm Dk 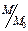
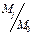
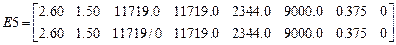 ,
,
Lx Ly Dx Dy Dm Dk 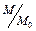
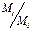
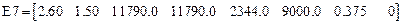
Матрицы L4, L5, L7: 
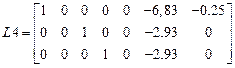 ,
,
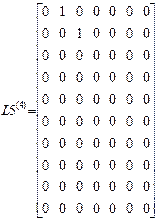 ,
, 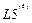 =
=  ,
, 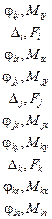
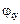 Δ
Δ 
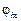
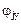 Δ
Δ 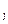
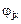
 Δ
Δ 
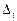
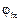
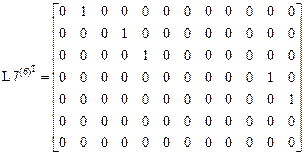
Компоненты первых пяти строк матрицы L7 – перемещения узлов.
Компоненты шестой и седьмой строк – усилия в элементах основной системы от заданной нагрузки.
Результаты расчета.
Матрицы реакций 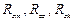
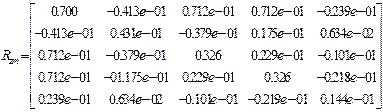 ,
,
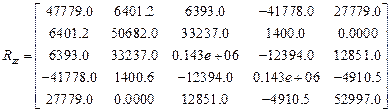 ,
,
R 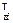 =
= 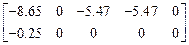 .
.
Коэффициенты жесткостей узлов элементов при повороте относительно координатных осей:
Четвертый элемент b(I,y)=37506.0, b(I,x)=24526.0, b(j,y)=8156.4, b(j,x)=12602.0, b(k,y)=28263.0, b(k,x)=21682.0.
Пятый элемент b(I,y)=37506.0, b(I,x)=24526.0, b(j,y)=8156.4, b(j,x)=12602.0, b(k,y)=28263.0, b(k,x)=21682.0.
Шестой элемент b(I,y)=13175.0, b(I,x)=47779.0, b(j,y)=13175.0, b(j,x)=47779.0, b(k,y)=13175.0, b(k,x)=47779.0.
Вектор собственных чисел λ и матрица V собственных векторов
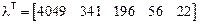 *e-08
*e-08
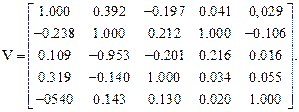
Матрица [ Z ] ,увеличенных в 1.0*E3 раз, перемещений узлов заданной системы
Z 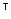 =
= 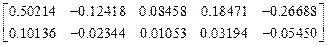 .
.
Матрица 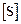 усилий в элементах заданной системы:
усилий в элементах заданной системы:
Четвертый и пятый элементы
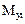
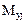
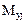
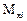
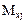
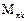
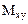
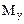
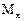
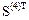 =
= 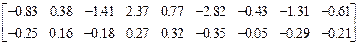
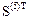 =
= 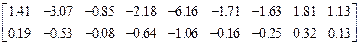
Шестой элемент основной системы
M 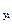 M
M 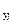 M
M 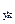 M
M 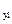 M
M 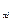 M
M 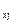 M
M 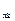 M
M 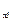 M
M 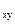 M
M 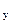 M
M 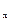
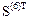 =
= 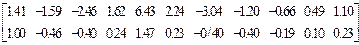 .
.
Положительные изгибающие моменты растягивают нижние волокна. Восьмые и девятые компоненты матриц 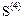 ,
, 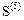 изги-
изги-
бающие моменты в центрах четвертого и пятого элементов. Десятые и одиннадцатые компоненты 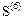 - изгибающие моменты в центре пятого элемента. Изгибающие моменты в узловых точках определяются как средние значения моментов в узлах смежных элементов.Компоненты первых строк матриц Z
- изгибающие моменты в центре пятого элемента. Изгибающие моменты в узловых точках определяются как средние значения моментов в узлах смежных элементов.Компоненты первых строк матриц Z 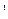 , S
, S 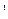 - перемещения и усилия от постоянной нагрузки, вторых – от временной нагрузки.
- перемещения и усилия от постоянной нагрузки, вторых – от временной нагрузки.
Изгибающие моменты на границе четвертого и шестого элементов относительно осей Y и X равны ((-0.83)+(-1.59)):2 = -1.21 кНм, (2.37+2.24):2 = 2,31 кНм; на границе пятого и шестого - (1.41+1.61):2 = 1.52 кНм, ((-2.18)+(-1.20)):2 = -1.69 кНм; на границе четвертого, пятого и шестого: ((-1.41) + (-3.06) + (-2.46)): 3 = -2.31 кНм, ((-2.82) +(-6.16)+(-3.04)): 3 = -4.01 кНм.
3.3 Расчет железобетонной плиты
на винклеровском основании.
На железобетонную плиту 8.00 х 4.00 х 0.30 м ., EJ 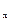 = EJ
= EJ 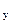 =94320 kHм, D
=94320 kHм, D 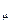 =18864 kHм, D
=18864 kHм, D 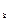 =72000 kНм,
=72000 kНм, 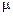 = 0.2 на винклеровском основании с коэффициентом упругой податливости 13012 кН/м
= 0.2 на винклеровском основании с коэффициентом упругой податливости 13012 кН/м 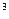 (рис.16) действуют: в центре плиты- сосредоточенные силы F
(рис.16) действуют: в центре плиты- сосредоточенные силы F 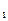 =1000.0 kH, F(t)
=1000.0 kH, F(t) 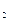 =0.8*Sin(20*t) kH; в точках с координатами 2.0х 0 м и -2.0х0 (начало в центре плиты) сосредоточенны силы F= 400 kH. Собственный вес плиты 7.5 кН/м
=0.8*Sin(20*t) kH; в точках с координатами 2.0х 0 м и -2.0х0 (начало в центре плиты) сосредоточенны силы F= 400 kH. Собственный вес плиты 7.5 кН/м  .
.
 Требуется определить усилия от статических возмущений и амплитудные значения усилий от динамических возмущений. Так как заданная система симметричная то в расчете можно рас смотреть четверть плиты (рис.17)
Требуется определить усилия от статических возмущений и амплитудные значения усилий от динамических возмущений. Так как заданная система симметричная то в расчете можно рас смотреть четверть плиты (рис.17)
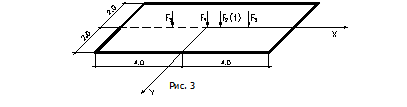
Рис.16
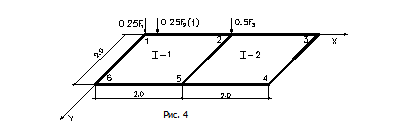
Рис.17
На выделенную часть действуют:
статические силы - F  =257.50 кН (узел 1), F
=257.50 кН (узел 1), F 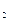 =215.00 кН (узел 2) и динамическая–F(t)=0.2*Sin(31*t) кН (узел 1).
=215.00 кН (узел 2) и динамическая–F(t)=0.2*Sin(31*t) кН (узел 1).
Основную систему получим наложением на выделенную часть тринадцати связей: линейной - на узел 1; связей, препятствующих повороту узла 2 относительно оси Y и его вертикальному перемещению; связей, препятствующих повороту узла 3 относительно оси Y и его вертикальному перемещению; связей, препятствующих повороту четвертого узла относительно оси Y, его вертикальному перемещению и связи, препятствующей его повороту относительно оси X; связей, препятствующих повороту пятого узла относительно оси Y, его вертикальному перемещению и повороту относительно оси X; связей, препятствующих вертикальному перемещению шестого узла и его повороту относительно оси X.
Полученная основная система (рис.17 )состоит из десяти элементов: шесть элементов четвертого типа (узлы 1, 2, 3, 4, 5, 6) и четыре элемента седьмого типа: седьмой и восьмой–элементы 1-
2-5-6 плиты и элемент основания, девятый и десятый – элемент 2-3-4-5 плиты и элемент основания.
M1 = 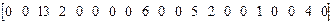 ,
,
EA/EJ 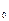 P1R1M/M
P1R1M/M 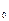 M
M  /M
/M 
E4 = 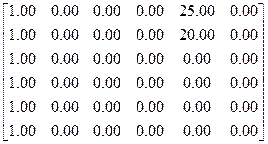
МатрицаЕ7
Lx Ly Dx Dy Dm Dk M/Mo M  /Mo
/Mo
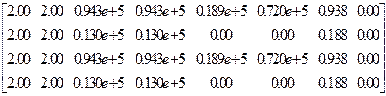
В матрицах L4 и L7 приведены только отличные от нуля компоненты. После компоненты указаны ее номер строки и номер столбца.
Матрица L4
Первый элемент: 1.00(1,1), -257.50(1,14), -0.80(1,15);
второй элемент : 1.00(2,3), -215.00(2,14), 0 (2,15) ;
третий элемент : 1.00(3,5), -7.50 (3,14), 0(3,15) ;
четвертый элемент: 1.00(4,7), -7.50 (4,14), 0(4,15) пятый элемент: 1.00(5,10), -15.00(5,14), 0(5,15) ;
шестой элемент : 1.00(6,12), -7.50(6,14), 0(6,15) .
Матрица L7
7-ой элемент: 1.00(2,1), 1.00(4,2), 1.00(5,3), 1.00(7,9), 1.00(8,10), 1.00(9,11), 1.00(11,12), 1.00(12,13);
8-ой элемент: 1.00(2,1), 1.00(5,3), 1.00(8,10), 1.00(11,12);
9-ый элемент: 1.00(1,2), 1.00(2,3), 1.00(4,4), 1.00(5,5), 1.00(7,6), 1.00(8,7), 1.00(9,8), 1.00(10,9), 1.00(11,10), 1.00(12,11);
10-ый элемент: 1.00(2,3), 1.00(5,5), 1.00(8,7), 1.00(11,10).
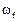 = 31.00 р/сек, EJ
= 31.00 р/сек, EJ 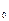 =1.00, m
=1.00, m 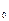 =1.00 .
=1.00 .
Компоненты первых строк матриц R 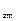 , R
, R 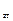 образуют матрицы:
образуют матрицы:
R 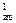 =
= 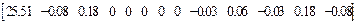
R 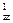 =
= 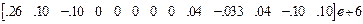
Матица R 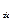 равна матрице:
равна матрице:
R 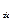 =
= 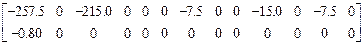 .
.
Первые три собственных числа образуют вектор :
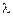
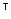 =[ 0.761 0.127 0.019 ]e-03,
=[ 0.761 0.127 0.019 ]e-03,
а одиннадцатое, двенадцатое и тринадцатое –вектор :
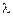
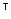 =[ 0.630 0.559 0.402 ]e-07.
=[ 0.630 0.559 0.402 ]e-07.
Им соответствуют собственные векторы :
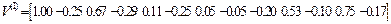
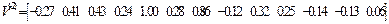
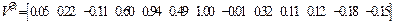
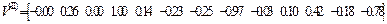
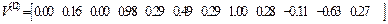
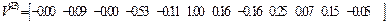
Матрица Z перемещений узлов заданной системы
( матрица основных неизвестных):
1; 0.840е-02 0.627e-04
2; -0.199e-02 -0.174e-04
3; 0.596e-02 0.392e-04
4; -0.238e-02 -0.184e-04
5; 0.144e-02 0.304e-05
6; -0.202e-02 -0.164e-04
7; 0.966e-03 0.115e-06
8; -0.388e-03 -0.242e-05
9; -0.157e-02 -0.137e-04
10; 0.473e-02 0.316e-04
11; -0.872e-03 -0.549e-05
12; 0.623e-02 0.467e-04
13; -0.135e-02 -0.108e-04
Матрица S усилий в элементах заданной системы.
Усилия в элементах четвертого типа от статических возмущений в заданной системе равны усилиям в элементах заданной системы. Амплитудные значения усилий от динамических возмущений отличны от нуля в первом и втором элементах и равны:
S  =-2.306 кН, S
=-2.306 кН, S 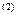 =-0.753 кН.
=-0.753 кН.
Усилия от статических и динамических возмущений в седьмом и девятом элементах образуют матрицы:
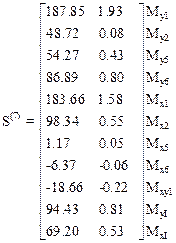
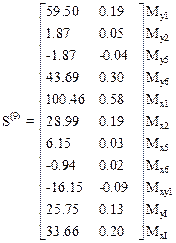
Интенсивность давления на основание определяется произведением жесткости основания на смещения линейных связей:
в узле 1 .130е5*(.840е-02 .626е-04) = ( .109 .008)е3кН/м  ,
,
в узле 2 .130е5*(.596е-02 .392е-04) = ( .077 .005)е3 кН/м 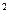 ,
,
в узле 3 .130е5*(.144е-02 .304е-05) = ( .018 0.001)е3кН/м 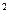 ,
,
в узле 4 .130е5*(.996е-03 .115е-06) = ( .013 .001)е2 кН/м 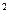 ,
,
в узле 5 .130е5*(.473е-02 .316е-04) = ( .058 .004)е3 кН/м 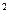 ,
,
в узле 6 .130е5*(.643е-02 .467е-04) = ( .083 .006)е3 кН/м 
4. Плоская задача теории упругости
4.1 Основная система. Исходные данные.
Определение усилий
Рассматриваемая система разбивается на прямоугольные и треугольные элементы. За основные неизвестные принимаются линейные – u(x,y), v(x,y) и угловые - dy/dx перемещения узлов. Положительные линейные перемещения – перемещения по направлению координатных осей, положительный угол поворота – поворот против хода часовой стрелки. Указанные перемещения – компоненты Ui, Vi, Fi, Uj, Vj, Fj, Uk, Vk, Fk, Ul,Vl, Fl m– ного (m = 1,2,…,n) столбца матриц L6, L8.
Компоненты i–того (i=n+1,n+2,…,f) столбца (f – число линейно независимых возмущений) – нули. Заданные силы переносятся на элементы четвертого типа с обратным знаком.
Если заданные силы вводить с обратным знаком в матрицы L6, L8, то соответствующие им усилия в заданной системе следует увеличить на заданные силы.
В прямоугольных элементах усилия N 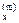 , N
, N 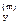 определяются для сторон, касательные N
определяются для сторон, касательные N 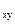 – в центре элемента:
– в центре элемента:
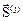 =[
=[ 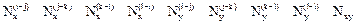 ].
].
В треугольных элементах усилия считаются постоянными
S 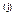 = [
= [ 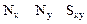 ].
].
В расчетах на динамические возмущения распределенные массы заменяются сосредоточенными узловыми массами. Их значения - компоненты пятых и шестых столбцов матрицы E4. Возмущения – компоненты матрицы L4. Упругие характеристики элементов основной системы задаются величинами:
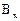 =
= 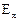 *h/
*h/ 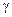 ,
, 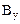 =
= 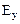 *h/
*h/ 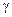 ,
, 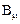 =
= 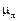 *
* 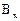 =
= 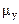 *
* 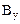 ,B=h*G,
,B=h*G,
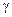 =1-
=1- 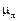 *
* 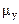 .
.
В случае плоской деформации вместо Ex, Ey вводятся
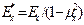 ,
, 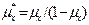 ,
, 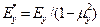 ,
, 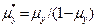
4.2 Расчет стенки на статические возмущения.
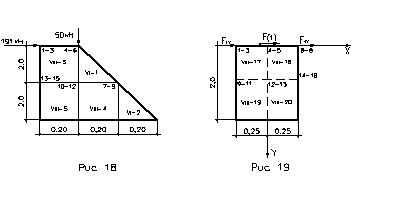
Определить усилия в защемленной по нижнему краю железобетонной стенке (рис.18 ) от статических равномерно распределенных по толщине сил: F 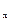 = 1.96 кН и F
= 1.96 кН и F 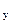 = 0.5 кН.
= 0.5 кН.
За масштабную жесткость примем B 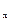 =B
=B 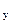 ,
, 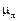 =
= 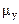 =0.167,
=0.167,
B= h*G = h*E/(2(1+ 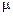 ))=B
))=B 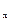 *
* 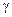 /(2(1+
/(2(1+ 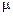 )) =0.43.
)) =0.43.
Заданную систему разбиваем на пять элементов. Число основных неизвестных равно пятнадцати.
M1=[ 0 0 15 2 0 0 0 0 0 0 0 1 2 0 0 2 0 2 0 3]
] 
Lx Ly Bx By Bm Bk
E6= 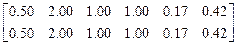 ,
,
E8= 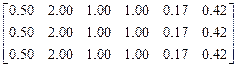 .
.
Компоненты матриц L6, L8 вводятся по столбцам. Ниже приведены ненулевые компоненты матриц. В скобках их место – номер столбца (порядковый номер основного неизвестного) и номер строки (порядковый номер перемещаемого узла).
МатрицаL6
Первый элемент: 1.00 (4,1), 1.00 (5,2), 1.00 (6,3), 1.00 (7,4)
1.00 (8,5), 1.00 (9,6), 1.00 (10,7), 1.00 (11,8), 1.00 (12,9)
Второй элемент: 1.00 (7,1), 1.00 (8,2), 1.00 (9,3).
Заданные возмущения отнесены к третьему элементу. Компоненты шестнадцатого и семнадцатого столбцов- нули.
Матрица L8
Третий элемент: 1.00 (1,1), 1.00 (2,2), 1.00 (3,3), 1.00 (4,4) 1.00 (5,5), 1.00 (6,6), 1.00 (10,7), 1.00 (11,8), 1.00 (12,9) 1,00 (13,10), 1.00 (14,11), 1.00 (15,12).
Заданным возмущениям соответствуют ненулевые компоненты шестнадцатого -1,91 (16,1) и семнадцатого -0.50 (17,5) столбцов.
Четвертый элемент: 1.00 (10,4), 1.00 (11,5), 1.00 (12,6)
1.00 (13,1), 1.00 (14,2), 1.00 (15,3).
Пятый элемент: 1.00 (7,4), 1.00 (8,5), 1.00 (9,6)
1.00 (10,1), 1.00 (11,2), 1.00 (13,3)
Увеличенные в EJo раз основные неизвестные равны :
1; 266.64 -0.002 8; 14.53 0.55
2; -72.50 1.74 9; -49.56 0.88
3; -158.10 -1.69 10; 56.12 -0.89
4; 261.83 -0.01 11; -9.04 1.01
5; -0.09 2.70 12; -49.74 0.89
6; -144.82 -1.51 13; 57.46 -0.94 7; 56.54 -0.82 14; -36.32 1.41
15; 51.30 0.83
Усилия в элементах заданной системы равны:
Элемент 1 Элемент 2
Nx Ny Sxy Nx Ny Sxy
-2.26 -16.32 -5.09 -2.25 -13.46 -2.20
-0.04 - 1.11 - 0.11 -0.03 - 0.16 -0.02
Nxij Nxjk Nxkl Nxli Nyij Nyjk Nykl Nyli Sx Элемент 3
-10.46 -1.03 -1.06 2.74 4.81 -4.56 5.97 18.04 -2.49
-0.10 -0.04 0.02 0.07 -1.01 -0,83 -0.49 - 0.14 -0.07 Элемент 4
-0.79 0.20 1.89 2.47 10.85 4.43 11.29 18.07 -0.70
-0.00 -0.04 -0.10 -0.04 -0.59 -0.49 -0.61 -0.69 -0.03 Элемент 5
0.62 -0.70 -0.23 1.27 -1.23 -7.18 -1.38 4.61 -2.89
0.06 0.01 -0.06 -0.03 -0.37 -0.26 -0.39 -0.50 -0.02 Так как заданные силы считались действующими на узлы третьего элемента, то усилия Nxij и Nyij в этом элементе будут равны Nxij =-10.46 + 1.96 = -8.50 от постоянной и Nyij =-1.01+0.50= -0,51 от временной нагрузок.
4.3 Расчет стенки на статические
и гармонические возмущения
Определить усилия в защемленной по нижней грани балки – стенки (рис.19) от статических сил F 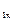 =F
=F 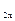 , = 1.00 кН, приложенных к верхним ребрам, и от динамической силы F(t) = 0.4*Sin (220*t) кН, действующей на сосредоточенную массу М = 2.00 т в средине верхней грани.
, = 1.00 кН, приложенных к верхним ребрам, и от динамической силы F(t) = 0.4*Sin (220*t) кН, действующей на сосредоточенную массу М = 2.00 т в средине верхней грани.
Высота балки 2.00 м, ширина – 0.50 м. Начало координат в средней точке верхнего левого ребра. Ось X направлена вправо, ось Y -вниз. B 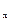 = B
= B 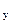 = 0.4E*10
= 0.4E*10 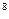 кН/м,
кН/м, 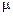 = 0.167.
= 0.167.
Основную систему представим системой, состоящей из четырех элементов восьмого типа 0.25*1.00 м. и шестнадцатью элементами четвертого типа. К последним относятся узлы, перемещения которых в заданной системе отличны от нуля. Основная система метода перемещений показана на рис.6. За масштабную жесткостную характеристику основной системы примем B 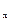 =0.40e+08 кН/м. Распределенные массы заменим сосредоточенными массами в узлах.
=0.40e+08 кН/м. Распределенные массы заменим сосредоточенными массами в узлах.
Так как от заданных возмущений перемещения левых узлов системы по величине равны перемещениям правых, а вертикальные перемещения средних равны нулю, то число основных неизвестных сокращается до десяти горизонтальные перемещения левых и правых узлов, вертикальные перемещения левых и правых узлов, угловые перемещения левых и правых узлов, горизонтальные перемещения средних узлов, угловые перемещения средних узлов. Матрицы исходных данных, с учетом сказанного, имеют вид:
M1=[ 0 0 10 2 0 0 0 0 0 16 0 0 5 2 0 0 1 0 0 0 4]
МатрицаE4
L EA/EJ 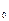 P1 R1 M/M
P1 R1 M/M 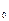 J
J 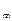 /M
/M 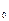
1; 1.00 0.00 0.00 0.00 0.138 0.00
2; 1.00 0.00 0.00 0.00 0.138 0.00
3; 1.00 0.00 0.00 0.00 0. 00 0.01
4; 1.00 0.00 0.00 0.00 0.138 0.00
5 1.00 0.00 0.00 0.00 0.138 0.00
6; 1.00 0.00 0.00 0.00 0.00 0.01
7; 1.00 0.00 0.00 0.00 2.28 0.00
8; 1.00 0.00 0.00 0.00 0.00 0.02
9; 1.00 0.00 0.00 0.00 0.276 0.00
10; 1.00 0.00 0.00 0.00 0.276 0.00
11; 1.00 0.00 0.00 0.00 0.00 0.02
12; 1.00 0.00 0.00 0.00 0.276 0.00
13; 1.00 0.00 0.00 0.00 0.276 0.00
14; 1.00 0.00 0.00 0.00 0.00 0.00
15; 1.00 0.00 0.00 0.00 0.552 0.00
16; 1.00 0.00 0.00 0.00 0.00 0.0
Матрица E8
L 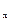 L
L 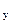 B
B 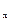 B
B 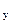 B
B 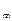 B
B 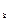 M/M
M/M 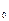 Mj/M
Mj/M 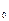
1; 0.25 1.00 1.00 1.00 0,167 0.430 0.00 0.00
2; 0.25 1.00 1.00 1.00 0.167 0.430 0.00 0.00
3; 0.25 1.00 1.00 1.00 0.167 0.430 0.00 0.00
4; 0.25 1.00 1.00 1.00 0.167 0.430 0.00 0.00
Матрица L4
1; 1.00 , 9*0 , - 1.00 , 0 2; 0, -1.00 , 10*0
3; 2*0, -1.00, 9*0 4; 1.00, 9*0, -1.00, 0
5; 0, 1.00, 10*0 6; 0, 0, -1.00, 9*0
7; 3*0, 1.00, 7*0, -0.40 8; 4*0, -1.00, 7*0
9; 5*0, 1.00 ,6*0 10; 6*0, -1.00, 3*0, -1.00, 0
11; 7*0,-1.00, 4*0 12; 5*0, 1.00, 6*0
13; 6*0, 1.00, 5*0 14; 7*0, -1.00, 4*0
15; 8*0, 1,00, 4*0 16; 9*0, -1.00, 2*0
М а т р и ц а L 8
Элемент 17
1.00 (1,1), -1.00 (2,2), -1.00 (3,3), 1.00 (4,4), -1.00 (5,5), 1.00 (10,6),
-1.00(11,7),-1.00(12,8),1.00(7,9),-1.00(9,10), 0.00(1,11), 0.00(4,12).
Элемент 18
1.00 (4,1), 1.00 (5,2), -1.00 (6,3), 1.00 (1,4), -1.00(3,5), 1.00 (7,6),
1.00 (8,7), -1.00(9,8), 1.00 (10,9), -1.00 (12,10).
Элемент 19
1.00(1,6), -1.00(2,7), -1.00 (3,8), 1.00 (4,9), -1.00 (6,10).
Элемент 20
1.0(4,6), 1,00 (5,7), -1.00 (6,8), 1.00 (1,9),-1.00 (3,10).
Отличные от нуля компоненты матрицы Rzm:
0.277 (1,1) 0.277 (2,2) 0.02 (3,3) 2.277 (4,4) 0.02 (5,5)
0.553 (6,6) 0.552 (7,7) 0.04 (8,8) 0.553 (9,9) 0.04 (10,10)
Компоненты верхнетреугольной части матрицы Rzz :
3.057 -0.299 -0.432 -2.928 0.421 0.943 -0.132 0.228 -1.072 -0.238
1.562 -0.057 -0.132 -0.074 0.132 0.502 0.014 0.298 0.032 0.094 0.421 -0.070 -0.228 0.014 -0.051 0.238 0.051
3.057 -0.432 -1.072 -0.298 -0.239 0.942 0.228 0.091 0.239 0.032 0.051 -0.228 -0.051
6,115 0.000 0.000 -5.857 0.000 3.123 -0.114 0.000 -0.149 0.183 0.000 -0.140 6.115 0.000 0.183
Отличные от нуля компоненты
Rzk -2.000 (1,1-21) -0.400 (4,22)
Вектор собственных чисел
V = [687.79 7.89 1.54 1.11 0.83 0.20 0.17 0.14 0.06 0.04 ] 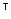
Матрица первых пяти собственных векторов
1.00 0.19 0.78 1.00 0.78 0.31 0.14 0.59 0.31 0.59
0.04 0.21 1.00 0.03 0.94 -0.27 0.08 -0.37 -0.27 -0.39
-0.03 -0.07 -0.76 0.02 -0.43 -0.21 0.11 0.95 -0.20 1.00
0.10 0.04 1.00 -0.03 0.08 0.05 0.02 0.39 0.03 0.29
-0,15 -0.00 -0.13 0.00 1.00 0.02 -0.00 0.08 0.04 0.24
Матрица [ Z ], увеличенных в EJo раз перемещений узлов заданной системы
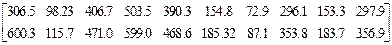
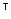
Матрицы усилий в элементах заданной системы
Nxij Nxjk Nxkl Nxli Nyij Nyjk Nykl Nyli Sxy
Элемент 17
-10.02 0.06 -4.00 4.29 10.08 0.10 11.08 25.33 -5.59
0.19 -1.51 -4.12 3.07 13.77 -0.25 13.05 29.36 -6,37 Элемент18
10.02 -4.29 4.00 -1.06 -10.08 -25.33 -11.08 -0.01 -5.59
- 0.19 -3.27 4.12 1.51 -13.77 -28.36 -13.05 0.25 -6.38 Элемент19
0.08 -3.88 6.10 8.29 35.51 -0.65 36.51 72.27 -5.29
0.81 -4.82 7.24 9.73 42.57 -0.81 43.68 86.32 -6.62 Элемент20
-0.08 -8.30 6.10 3.88 -35.51 -72.27 -36.51 0.65 -5.29
0.81 -9.72 -7.30 4.82 -42.57 -86.32 -43.66 0.81 -6.62
Заключение
В работе рассмотрены вопросы определения напряженно деформированного состояния линейно деформируемых систем, находящихся под действием статических и динамических возмущений.
В первой части пособия даны основные теоретические положения по определению усилий и перемещений в элементах заданной системы. Получены уравнения для определения основных неизвестных : перемещений, скоростей и ускорений узлов основной системы методом перемещений. Определены исходные данные и порядок их вода для решения задачи на ЭВМ по программе DINAM.
Во второй части пособия рассмотрены вопросы определения усилий и перемещений в стержневых системах. Напряженно деформированное состояние стержневых систем определяется точно с учетом и без учета деформации сдвига и по деформированной схеме при постоянных продольных силах. Рассмотрены вопросы определения усилий от гармонических возмущений в диссипативных системах. Даны примеры расчета стержневых систем на упругом винклеровском основании на статические и гармонические возмущения, определения усилий и перемещений от неточностей изготовления и смещений связей заданной системы, определения усилий и перемещений от температурных возмущений.
В третьей части определяются напряженно деформированные состояния тонких плит от статических и динамических возмущений. Задача решается методом перемещений. Заданная система разбивается на прямоугольные и треугольные элементы. Поверхности изгиба задаются неполным бикубическим полиномом (прямоугольный элемент) и полиномом с десятью параметрами (треугольный элемент). Заданные нагрузки заменяются узловыми силами. Полученные решения приближенные. Степень приближения зависит от числа и вида элементов основной системы. На печать выдаются изгибающие моменты в узловых точках, изгибающие и крутящие моменты в центрах элементов основной системы. В расчетах плит на упругом основании основание представляется элементами идентичными элементам плиты. В расчетах на динамические возмущения приведенная масса основания присоединяется к массе расположенного на нем элемента плиты.
В четвертой части пособия рассмотрены вопросы определения напряжений и деформаций систем, состоящих из плоско напряженных элементов. При выборе основной системы элемент заданной системы разбивается на прямоугольники и треугольники. За основные неизвестные принимаются линейные и угловые перемещения узлов в плоскости элемента. Заданные силы заменяются узловыми. В динамических расчетах распределенные массы заменяются узловыми массами. Нормальные усилия определяются для средин сторон четырех угольника. Сдвигающие усилия – в средней точке. В треугольном элементе усилия принимаются постоянными.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Р. Клаф Дж. Пензиен. Динамика сооружений.–М.Стройиздат. 1979.
2. Р.Ливсли . Матричные методы строительной механики. –М.Стройиздат. 1980
3. А.Ф.Смирнов. Методы расчета стержневых систем, пластин и оболочек с использованием ЭВМ. ч.1 и 2. М. 1976
4. А.Ф.Смирнов, А.В.Александров и др. Динамика и устойчивость сооружений,-Москва, 1996.
5. А.М.Масленников. Расчет строительных конструкций численными методами. Л. 1987.
6. Д.К.Фадеев,А.Н.Фадеева. Вычислительные методы линей-ной алгебры. М,Л
7. В.И.Роев. Расчет плоских рамных систем на динамические нагрузки по деформированной схеме. Изв.вузов, Строительство и архитектура, № 1, стр. 36-39, 1990
8. В.И.Роев. Линейно деформируемые системы. Расчет методом пермещений в матричной форме, -Новосибирск, 1993
9. В.И.Роев . Расчет стержневых систем на динамические нагрузки методом перемещений, - Новосибирск, 1993
10. В.И.Роев . Устойчивость упругих стержневых систем.-Новосибирск 1997
11. Г.И.Гребенюк, В.И.Роев. Влияние деформации сдвига и продолных сил на динамические характеристики стержневых систем. Изв.высших учебных заведений., Строительство. №6, стр. 19-24, 1998
12. Г.И.Гребенюк, В.И.Роев, М.С.Вешкин. Алгоритм численного расчета стержневых систем при импульсных нагрузках Труды НГАСУ,т.2. № 2(4), 1999
13. Г.И.Гребенюк, В.И. Роев. О расчете диссипативных систем с частотно независимым внутренним трением. Изв. высших учебных заведений. Строительство. №7,2002, стр.21-27.








