Определение усилий от возмущений, изменяющихся
во времени по произвольному закону(рис.13)
На систему на рис. 6 действуют силы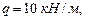 
F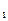 
(t)=(10+5 
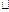Sin(21.372 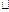t)) кН (0 
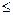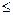t 0.147 с),
F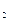 
(t)=(15+1 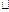Sin(10.686 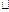t)) кН (0 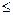t 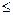0.588 с) ,
F = 1500 .
Определить усилия в моменты времени (0+0.0368n) с.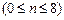 
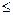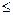и (.294+.0735n) с. (0 n 4).
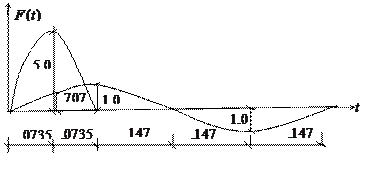
Основная система метода перемещений на рис. 2.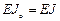 
. Время действия заданных возмущений разбиваем на три интервала длиной 0.147, 0.147, 0.294 с. Каждый интервал делим на 4 отрезка.
Исходные данные:
.
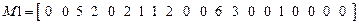Матрицы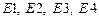 
такие же как в расчетах на гармонические возмущения.
,
,
,
,
.
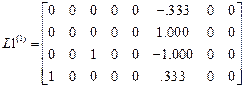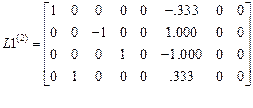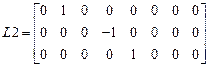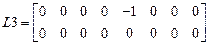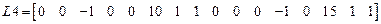Матрица начальных условий первого интервала (компоненты первого столбца – перемещения узлов, второго – скорости)
.
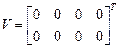Матрица длин интервалов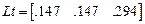 
.
Матрица значений нагрузок в начале средине и конце интервалов
.
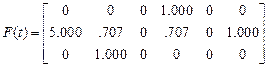Матрица дополнительных перемещений и скоростей, задаваемых в начале последнего интервала
.
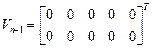Значения масштабной жесткости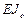 
и масштабной массы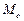 
.
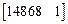
Результаты расчета:
Матрицы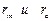 
такие же как в расчетах на гармонические возмущения.
.
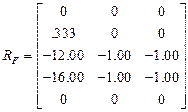Вектор собственных чисел и матрица собственных векторов такие же как в расчетах на гармонические возмущения.
Векторы частот и периодов собственных колебании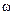 
,
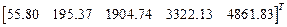Первый интервал.
Матрицы ускорений и увеличенных в 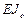раз перемещений узлов:
, 
.
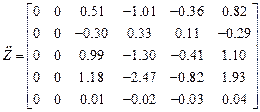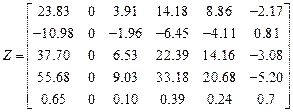Матрицы концевых усилий
,
,
,
,
.
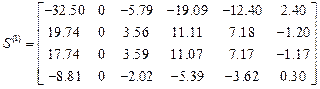
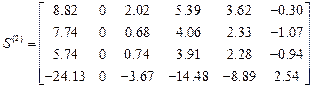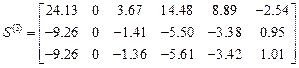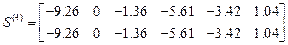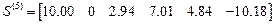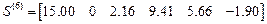Компоненты первых столбцов матриц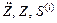 
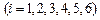– ускорения, перемещения, концевые усилия от статических нагрузок. Компоненты остальных столбцов–ускорения, перемещения и концевые усилия от динамических возмущений в моменты времени, соответствующие границам отрезков.
Второй интервал. Матрица начальных условий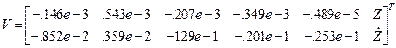 
.
Матрицы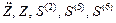 
,
,
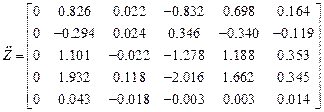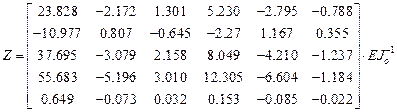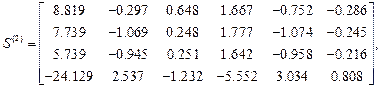
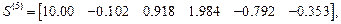
Определение усилий от мгновенного импульса
Определить по деформированной схеме с учетом деформации сдвига усилия в системе на рис. 6, вызванные сосредоточенными мгновенными импульсами
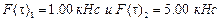
в моменты времени 0.01395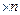 
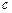(n = 0, 1, 2, …,8). Жесткости элементов системы и величины масс такие же как и в расчетах на нагрузку, изменяющуюся во времени по произвольному закону. Основная система на рис.7.
Заданное время разделим на два интервала. Число отрезков в интервале примем равным четырем.
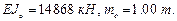
Решение задачи состоит из двух этапов. На первом этапе определяются скорости узлов – начальные условия. На втором этапе заданная система рассчитывается на собственные колебания.
Первый этап. Компоненты шестых столбцов матриц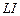 
- концевые усилия в элементах основной системы от заданных импульсов. Они определяются как усилия от статической нагрузки. Компоненты седьмых столбцов принимаются равными нулю. В матрице 
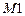мгновенному импульсу соответствует 
.
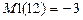Исходные данные: Матрицы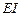 
такие же, как в предыдущей задаче.
, 
,
.
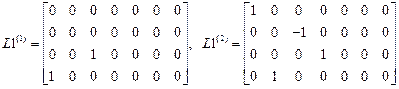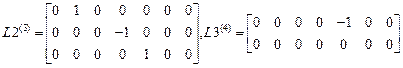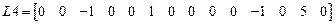Результаты расчета. На печать выдаются матрицы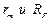 
. 
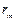такие же как в задаче на гармонические возмущения.
.
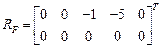Из уравнения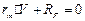 
определяется матрица обобщенных координат и их первых производных в момент исчезновения импульсов 
.
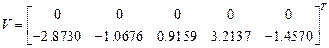После нажатия клавиши 
осуществляется переход ко второму этапу.
Второй этап расчета.
На экран выдаются исходные данные первого этапа расчета и матрица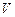 
. В матрице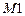 
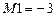заменяется на 
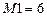. По желанию пользователя в матрицах 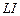компоненты столбцов, соответствующих концевым усилиям от статических и динамических возмущений можно откорректировать. В рассматриваемом примере это компоненты шестых и седьмых столбцов. Для того, чтобы определить усилия от статической нагрузки 
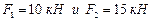компоненты шестых столбцов матриц 
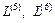приняты равными 10 и 15 соответственно. Начальными условиями являются компоненты матрицы .
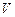Результаты расчета. На печать выдаются матрицы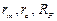 
, матрицы обобщенных координат, их вторых производных, концевые усилия в моменты времени, соответствующие границам отрезков, начальные условия на границах интервалов, векторы частот и периодов собственных колебаний.
На границах отрезков первого интервала концевые усилия первого элемента образуют матрицу
.
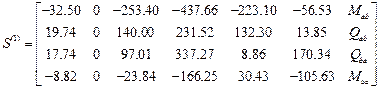На границах отрезков второго интервала концевые усилия образуют матрицу
.
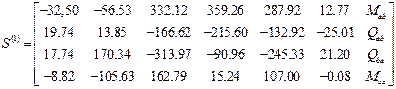Начальные условия второго интервала определяются матрицей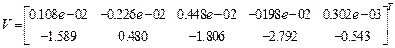 
.
Матрица перемещений и скоростей в конце второго интервала имеет вид: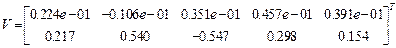 
.