Определение критического значения нагрузки
Для системы на рис.9 определить критическое значение параметра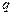 
заданной нагрузки. Жесткости элементов 
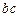и 
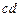равны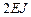 
, жесткости остальных - 
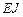. Основная система метода перемещений на рис.10. Третья связь наложена на сечение 
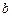стержня 
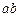в связи с тем, что в расчетах на устойчивость по программе 
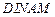каждый элемент основной системы должен деформироваться хотя бы от смещения одной связи.
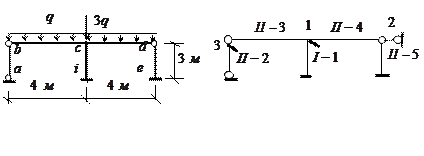
Рис.9 Рис.10
Продольные силы определяются расчетами на прочность. Они равны: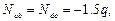 
, 
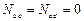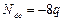. За масштабную жесткость 
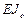примем 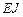, за ведущий элемент - элемент 
.
,
,
.
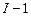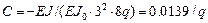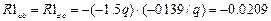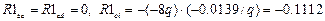Исходные данные:
,
,
,
, 
,
, 
.
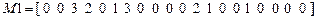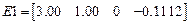
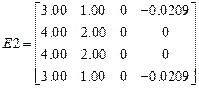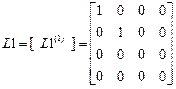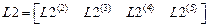
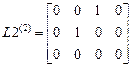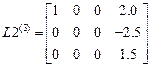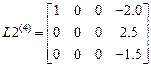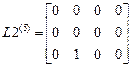Результаты расчета: Критическое значение коэффициента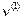 
продольной силы равно 2.794. Вектор основных неизвестных, соответствующий первой форме потери устойчивости
.
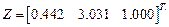Вектор отношений критических значений продольных сил к масштабной жесткости 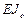равен
.
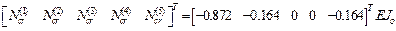Следовательно: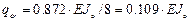 
кН/м.
Приведенные длины образуют вектор
.
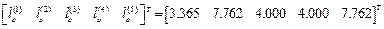Примечание: Четвертые столбцы матриц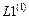 
, 
, 
, 
, 
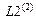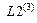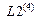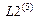оставлены после первого этапа расчета для того чтобы не перебивать исходные данные. С той же целью оставлены 
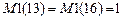. В расчете на устойчивость можно принять 
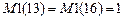, а в блоки матриц 
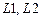вводить по три столбца.
Определение усилий в балке на упругом основании
Определить усилия в балке на упругом винклеровском основании (рис. 11). Ширина поперечного сечения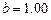 
м., высота 
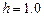м., 
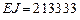кН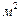 
, коэффициент упругой податливости основания 
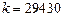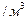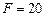кН 
, 
кН,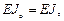 
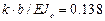
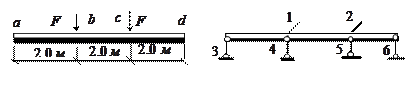
Рис.11 Рис.12
Основная система на рис.12. Она состоит из пяти элементов. Стержень 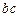- 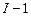, стержень - 
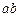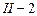, стержень - 
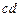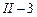, узлы 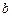и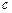 
- 
.
, 
.
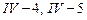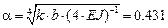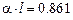Введем групповые неизвестные :
.
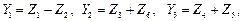
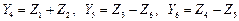Так как нагрузка симметричная, то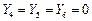 
и исходные данные имеют вид:
,
,
,
,
,
,
.
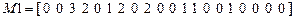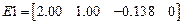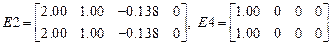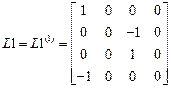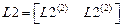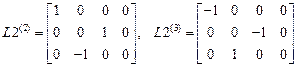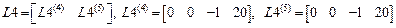Результаты расчета:
,
,
/ , 
,
, 
.
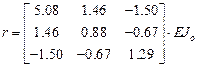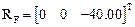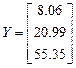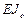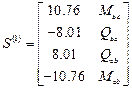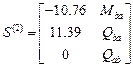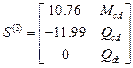2.3 Динамические возмущения
Определение усилий от гармоничес ких возмущений.
Система на рис. 6 находится под действием сил:
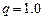кН/м,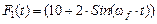 
,
, 
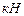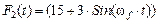
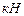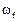=53.00 р/с,
.
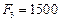
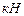В сечении 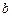находится точечная масса 1 т, в сечении 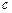- точечная масса 1.5 т. Интенсивность распределенной массы балки – 0.0365 т/м, интенсивность распределенного момента инерции массы –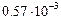 
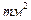. Требуется определить с учетом деформации сдвига по деформированной схеме усилия от статических составляющих заданных нагрузок, амплитудные составляющие от гармонических составляющих и их возможных сочетаний. Определить частоты и векторы форм собственных колебаний. Основная система на рис. 7
Исходные данные: В расчетах по деформированной схеме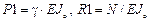 
. Относительный угол сдвига 
( 
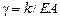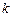- коэффициент формы поперечного сечения).
, 
.
,
,
.
.
.
.
.
,
.
.
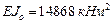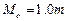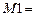
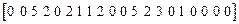
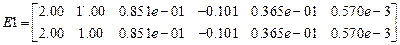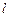
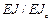
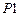
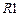
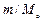
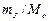
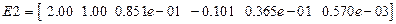
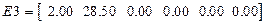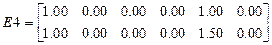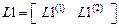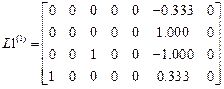
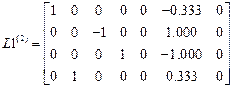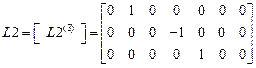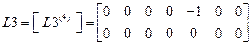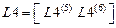
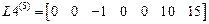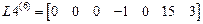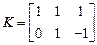Число определяемых собственных чисел 5.
.
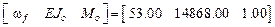Результаты расчета:
,
,
.
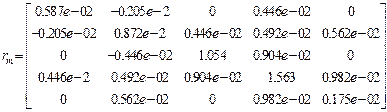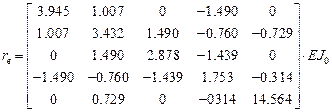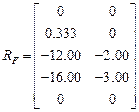Вектор собственных чисел:
,
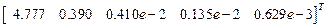Матрица собственных векторов:
.
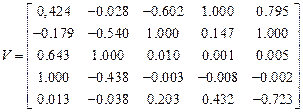Матрица основных неизвестных:
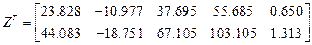
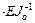
Матрицы концевых усилий: ,
,
,
,
,
.
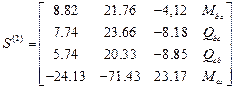
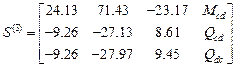
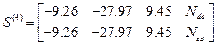
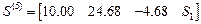
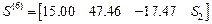