В элементах седьмого типа (прямоугольный элемент плиты)
,
.
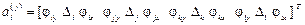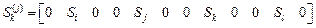
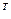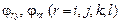– углы поворота узла 
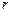относительно осей 
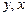соответственно. 
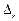– линейное перемещение узла 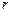. Положительные 
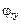– повороты по ходу часовой стрелки, положительные 
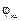– повороты против хода часовой стрелки, если смотреть в начало координат. Положительные 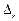направлены вниз и растягивают нижние волокна. 
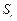– концевое усилие, равное по величине узловой силе, но направленное в обратную сторону. Для сокращения трудоемкости ввода концевые усилия смежных объединяются в одно и прикладываются к элементу четвертого типа. Тогда 
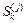будет нулевым вектором.
В элементах пятого ( треугольный элемент плиты)
, 
.
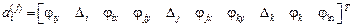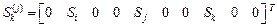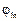– угол поворота узла 
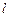в плоскости, нормальной к прямой 
.
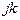В элементах восьмого типа (прямоугольный элемент плоской задачи)
,
.
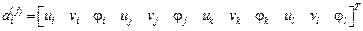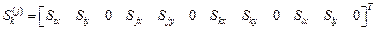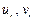– перемещения узлов в направлении осей 
. 
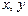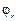– угол поворота узла. Положительные перемещения совпадают с положительными направлениями локальных осей. Положительный угол поворота – поворот против хода часовой стрелки, если смотреть в начало координат. 
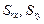– концевые усилия в узле.
Положительные концевые усилия направлены в сторону положительных локальных осей. Они по величине равны узловым силам и направлены в обратную сторону.
В элементах шестого типа (треугольный элемент плоской задачи)
,
.
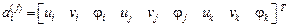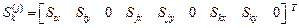4. Матрица сочетаний. Матрица сочетаний заданных возмущений – прямоугольная матрица. Число ее строк равно числу независимых заданных возмущений. Число столбцов – числу сочетаний заданных возмущений, интересующих пользователя. Компонента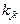 
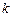‑того столбца и 
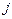‑той строки равна единице, если заданное возмущение учитывается в 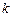‑том сочетании и равно нулю, если не учитывается. Применяя матрицу сочетаний 
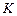усилия можно определять от единичных значений заданных возмущений, а их величины водить как компоненты матрицы 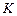. Если матрицу 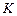принять нулевой ( 
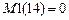), то на печать будут выданы усилия от каждого возмущения в отдельности.
5. Прочие исходные данные. В расчетах на гармонические возмущения запрашивается частота заданных возмущений, масштабная жесткость и масштабная масса, число собственных чисел, интересующих пользователя программы и точность с которой определяются собственные числа. В расчетах на возмущения, изменяющиеся во времени по произвольному закону, запрашивается число интервалов, на которые разделено время действия возмущений и число отрезков, на которые разделен интервал. Запрашивается также матрица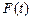 
заданных возмущений. Она состоит из блоков. Число блоков рано числу интервалов, на которое разбито время действия возмущений. Компоненты 
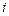‑того столбца ( 
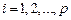) каждого блока равны значению 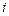‑того возмущения в начале, средине и конце интервала. 
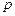– число заданных возмущений. Время действия возмущений разбивается на интервалы так, чтобы на протяжении интервала на графиках возмущений не было ни перегибов, ни переломов, ни скачков. Усилия в заданной системе определяются на границах отрезков, на которые разделен интервал.
6. Пространственные стержневые системы. В расчетах пространственных систем стержень представляется четырьмя элементами: элементом, изгибаемом в плоскости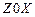 
, элементом, изгибаемом в плоскости 
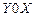, элементом, работающем на растяжение (сжатие), и скручиваемым элементом. Согласно принятому порядку нумерации элементов первые два имеют порядковые номера 
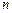и 
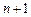, а третий и четверты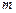й - 
и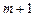 
. Такая нумерация создает определенные визуальные неудобства при определении напряженно-деформируемого состояния стержня.
Для того, чтобы получить компактную картину усилий в стержне элемент, работающий на растяжение (сжатие), и скручиваемый элемент можно объединить в один комбинированный элемент с матрицами
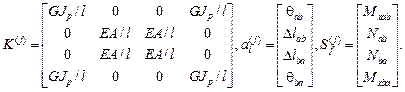
для стержня с защемленными концами;
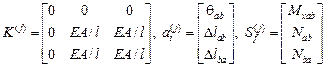
для стержня с защемленным и шарнирно опертым концами.
Матрицы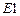 
и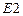 
для комбинированных элементов, в этом случае, имеют вид
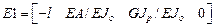
для стержня с защемленными концами.
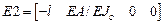
для стержня с защемленным и шарнирно опертым концами.
В случае динамических возмущений пятые и шестые компоненты 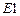и 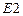комбинированного элемента равны нулю.
Знак “-“ перед l – признак комбинированного элемента.
Если в расчетах нужно учесть стесненное кручение, то стержень нужно задать четырьмя элементами: два изгибаемых, один растянутый (сжатый) и элемент в состоянии стесненного кручения. Матрицы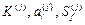 
для элемента в состоянии стесненного кручения определяются в обычном порядке, а в матрице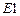
строка, соответствующая элементу в состоянии стесненного кручения имеет вид:
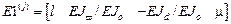
(знак “ – “ перед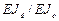 
- признак стесненного кручения). 
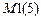=0.
В комбинированном элементе жесткость на кручение принимается равной нулю.
7. Решение системы линейных алгебраически уравнений. Для решения системы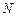 
линейных алгебраических уравнений с 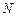неизвестными нужно принять 
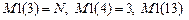равным числу свободных членов, 
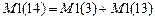, а остальные компоненты 
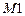равными нулю и ввести по столбцам компоненты матрицы коэффициентов при неизвестны и компоненты матрицы свободных членов.
8. Определение собственных чисел и собственных векторов квадратной матрицы. Для определения собственных чисел и собственных векторов квадратной матрицы порядка 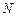нужно принять 
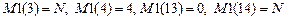, а остальные компоненты 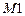равными нулю и ввести по столбцам компоненты матрицы.
1.8. Ввод исходных данных
Перед вводом исходных данных машина запрашивает имя файла результатов расчета, Затем запрашивается шифр задачи. 7При диалоговом вводе шифр должен быть меньше 100000, при файловом вводе – больше 100000. После ввода шифра запраши-
вается имя файла, в котором будут храниться исходные данные (файл исходных данных).
Ввод исходных данных осуществляется в последовательности: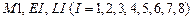 
и прочие данные. Перед вводом каждой из перечисленных матриц следует зарос: нужны ли комментарии по ее составлению и вводу? По окончании ввода каждой матрицы после нажатия 
на экране высвечиваются блоки матрицы и предоставляется возможность исправит допущенные ошибки.
После ввода исходных данных предлагается посмотреть исходные данные и результаты расчета. Исходные данные сохраняются до начала решения следующей задачи. Если при просмотре будет обнаружена ошибка в исходных данных, или расчет нужно повторить при других исходных данных, то после нажатия 
вводится 1. На экран последователь выводятся исходные данные и в них можно ввести необходимые коррективы.
При файловом вводе коррективы вносятся в файл исходных данных.
1.9. Результаты расчета
Результаты расчета (система канонически уравнений, матрица основных неизвестных, собственные числа и собственные векторы, усилия в элементах заданной системы от заданных возмущений или их сочетаний) хранятся в файле результатов расчета.
Положительные изгибающие моменты в элементах первого и второго типа направлены по ходу часовой стрелки. Положительные продольные силы растягивают стержень. Положительный крутящий момент направлен по ходу часовой стрелки относительно внешней нормали к поперечному сечению.
У изгибающих моментов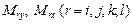 
элементов плит первый индекс – номер узла, второй – ось, относительно которой действует момент. Положительные изгибающие моменты растягивают нижние волокна. Крутящий момент определен в
среднем сечении прямоугольного элемента и в средине диагонали треугольного элемента.
У нормальных усилий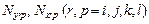 
плоских прямоугольных элементов – ось, в направлении которой действует сила, второй и третий – сторону прямоугольника, в средине которой действует усилие. Сдвигающее усилие 
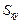определено в центре элемента.
Нормальные усилия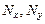 
и сдвигающее – 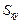определе
ны в центре плоского треугольного элемента.
2. Кинематически неопределимые стержневые системы
2.1. Основная система . Исходные данные
Основная система получается из заданной наложением на ее узлы угловых и линейных связей.
Угловые связи накладываются на жесткие узлы. Число и положение линейных определяется из условия: шарнирно‑стержневая система, полученная из заданной удалением стержней, деформацию растяжения (сжатия) которых нужно учесть, после наложения линейных связей должна превратится в кинематически определимую систему. За узел может быть принято любое поперечное сечение стержня.
Элементы основной системы подразделяются на четыре типа: стержни постоянного поперечного сечения с защемленными концами (первый тип), стержни с одним защемленным и другим шарнирно–опертым концом (второй тип), изгибаемые элементы с цилиндрическими шарнирами на концах(жесткость на изгиб принимается равной нулю) и стержни, работающие на растяжение (сжатие), ( третий тип), элементы основной системы , деформацией которых можно пренебречь, (элементы четвертого типа). Если для какого-то стержня нужно учесть влияние и деформации изгиба и растяжения (сжатия), то в основной системе он представляется двумя элементами.
К исходным данным относятся матрицы M1, E1, E2, E3, E4, L1, L2, L3, L4.
M1 – матрица‑строка. Ее первый, второй, десятый, одиннадцатый, семнадцатый, восемнадцатый, девятнадцатый двадцатый компоненты равны нулю. Третий – равен числу основных неизвестных; четвертый – двум (признак метода); пятый – числу элементов в состоянии стесненного кручения; шестой, седьмой, восьмой и девятый - числу элементов первого, второго, третьего и четвертого типов соответственно. Двенадцатый – определяет тип заданного возмущения: в расчетах на статические возмуще
ния – 1, в расчетах на гармонические и статические – 5, в расчетах на динамические возмущения, изменяющиеся во времени по произвольному закону, – 6, в расчетах на динамические возмущения с учетом внутреннего трения и демпфирования – 7, в расчетах на мгновенный импульс: первый этап – (-3), второй этап – 6, в расчетах на устойчивость – 2. M1(13) – число заданных возмущений. M1(14) – число сочетаний заданных возмущений. M1(15) =0. Если в расчетах осуществляется оптимизация конструкции, то M1(15) >0.
Составление матриц E1, E2, E3, E4, L1, L2, L3, L4 рассмотрено в комментариях к программе. Обращение к комментариям возможно на любом этапе ввода исходных данных. Их составление подробно рассмотрено в параграфе (1.7) и [6].
2.2 Статические возмущения
Определение усилий с учетом деформации сдвига.
Определить усилия в системе на рис.6 от нагрузок: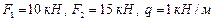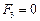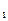 
, 
.
F 
, F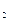 
-постоянная нагрузка, q-временная.
Балка – двутавр №30.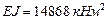 
, 
,
,( 
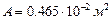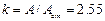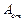-площадь стенки двутавра).
Жесткость стойки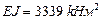 
, 
.
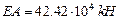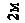
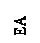
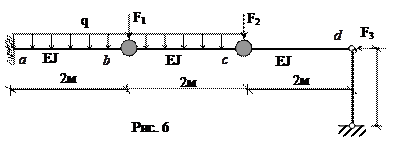
Основная система метода перемещений на рис. 7
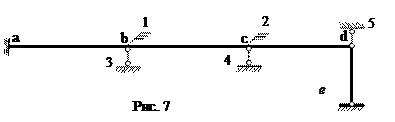
За положительные смещения угловых связей приняты повороты по ходу часовой стрелки. Положительные перемещения линейных связей направлены вниз.
Концевые усилия (изгибающие моменты и поперечные силы в концевых сечениях, а также силы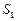 
и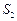 
, уравновешивающие 
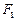и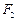 
) показаны на рис. 8. Положительные изгибающие моменты направлены по ходу часовой стрелки
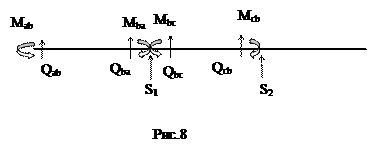
Основная система состоит из восьми элементов. Стержни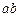 
и 
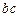– элементы первого типа с номерами 
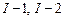. Стержень 
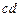– элемент второго типа номер 
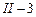. Стержень 
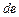в расчете представляется двумя элементами третьего типа. Элементом, работающим на растяжение (сжатие) номер 
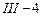и изгибаемым элементом - номер 
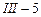. Узел 
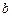с сосредоточенной силой – номер 
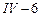. Узел 
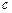с сосредоточенной силой
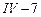. Так как стержень 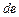не загружен, то элемент 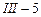можно в расчет не вводить. 
.
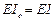Исходные данные:
Матрица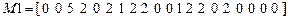 
.
Матрицы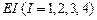 
. Число строк равно числу элементов данного типа.
,
,
, 
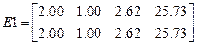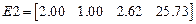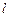
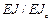
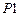
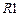
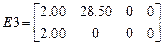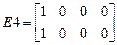
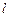
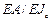
Матрицы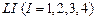 
. Матрицы состоят из блоков.Число блоков равно числу элементов данного типа. Число строк зависит от типа элемента. В элементе первого типа – четыре, в элементе второго – три , в элементе третьего – две, в элементе четвертого одна.
,
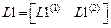L1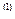 
= 
,
.
.
,
.
,
.
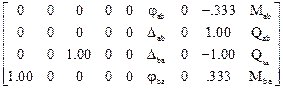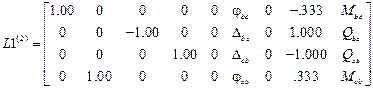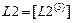
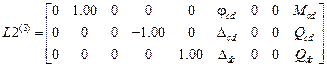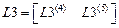
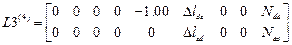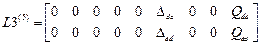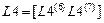
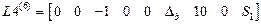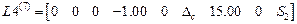Если бы в узле 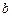был приложен сосредоточенный момент , а не сосредоточенная сила, то в 
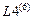первая компонента равнялась бы углу поворота сечения .
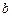Матрица сочетаний
.
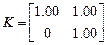Если бы нужно было определить усилия от временных нагрузок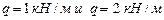 
, то
.
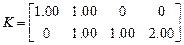Компоненты матриц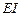 
, 
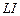и 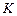вводятся по столбцам.
После ввода исходных данных на экран монитора выводятся исходные данные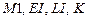 
и результаты расчета – матрицы: 
.
,
,
,
,
,
.
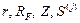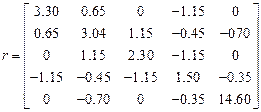
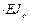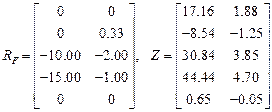
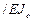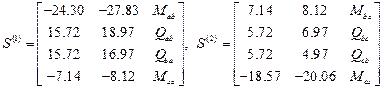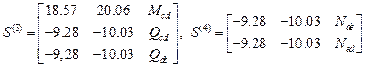
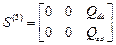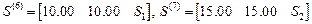Если усилия определяются без учета деформации сдвига,
то P1=R1=0/
Определение усилий от смещений связей.
В системе на рис.6 сечение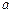 
двутавра отторцовано под углом 
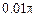рад. от нормали к оси стержня по ходу часовой стрелки. Элемент 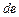изготовлен длиной 
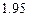м. Сечени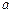е пе
реместилось вверх на 0.05 м. Определить усилия от заданных возмущений.
Усилия определяются от каждого возмущения отдельно.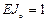 
. Возмущения, вызванные неточностью изготовления, вводятся с обратным знаком. 
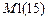равно нулю. За основную систему примем систему, полученную из заданной наложением линейной связи на узел 
.
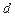Исходные данные:
,
,
,
.
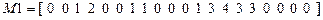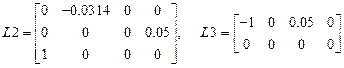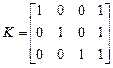Результаты расчета:
,
,
, 
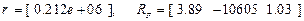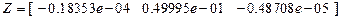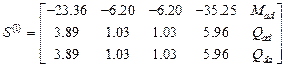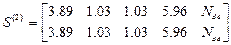
Определение усилий по деформированной схеме.
| |
| |
Определить усилия в системе на рис.6 по деформированной схеме если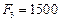 
кН. Деформацией сдвига пренебрегаем.
Из условий равновесия следует, что в поперечных сечениях стержней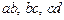 
продольная сила 
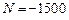кН. Коэффициенты продольной силы
, 
, 
, 
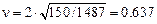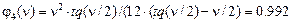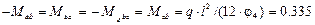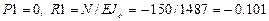
Исходные данные: Матрица 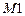такая же как в примере 1.
,
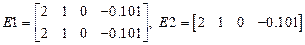матрицы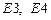 
такие же как в примере 1. В матрице 
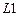моменты 0,333 в концевых сечениях нужно заменить на 0.335. Матрица сочетаний 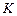такая же как примере 1.Результаты расчета:
,
.
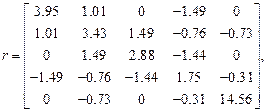
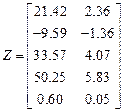
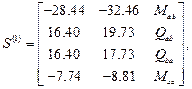
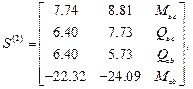
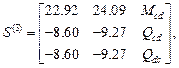
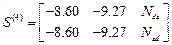