Стесненное кручение.
В состоянии стесненного кручения элемент основной системы относится к элементам первого типа. Его концевые сечения не могут вращаться и не могут депланировать.
,
,
,
.
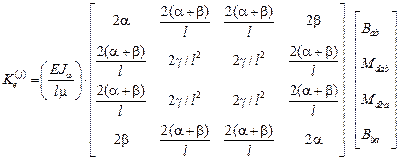
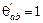
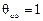
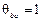
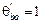
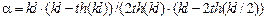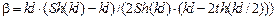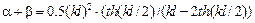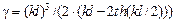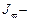главный секториальный момент инерции поперечного сечения, 
, 
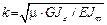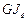- крутильная жесткость. Для стержней открытого профиля 
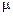= 1, для стержней закрытого профиля 
, 
,
, 
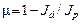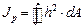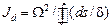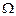- удвоенная площадь, ограниченная средней линией контура, 
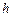- расстояние от центра кручения до касательной к контуру.
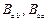- бимоменты в сечениях 
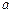и 
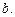
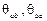- углы поворота сечени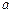й и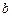 
относительно оси стержня. 
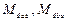- полные крутящие моменты в сечениях 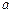и .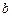
Вектор концевых усилий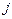 
того элемента основной системы от заданных возмущений равен вектору
.
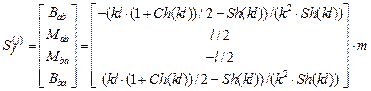Вектор перемещений концевых сечений от единичного смещения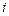 
- той связи основной системы имеет вид :
.
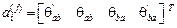Вектор концевых усилий в заданной системе от заданных статических возмущений определяется суммой
.
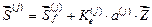Влиянием сил инерции, соответствующих депланации поперечных сечений и кручению, пренебрегаем. Поэтому концевые усилия в заданной системе от динамических возмущений определяются так же как и от статических возмущений,но вместо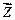 
подставляется вектор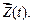 
Положительный угол закручивания и крутящий момент направлены по часовой стрелке, если смотреть на сечение со стороны внешней нормали. При определении знака бимомента и депланации , для каждого концевого сечения выбирается правая координатная система с началом в центре кручения. Ось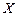 
параллельна оси стержня и направлена к его противоположному концу. Ось 
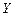параллельна стенке условного двутавра. Положительный бимомент растягивает ближние к наблюдателю волокна верхней полки. Наблюдатель смотрит на двутавр с положительного направления оси 
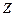. Для наблюдателя смотрящего на двутавр сверху (снизу) верхний (нижний) момент положительного бимомента направлен по часовой стрелке. Согласно принятому правилу знаков бимоменты двух смежных сечений имееют разные знаки. Положительный скручивающий момент направлен по часовой стрелке относительно внешней нормали концевого сечения со старшим порядковым номером.
1.3. Тонкие плит ы
Рассматривается расчет тонких плит для которых справедливы гипотезы Кирхгова-Лява. Материал плит считается идеально упругим и ортотропным. Плита разбивается на прямоугольники и прямоугольные треугольники. При принятии гипотезы о нормальном элементе каждый узел имеет три степени свободы: прогиб срединной плоскости и два угла поворота в двух взаимно перпендикулярных направлениях. За положительный принят прогиб, направленный вниз (положительное направление оси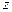 
). Положительные углы поворота отсчитываются против хода часовой стрелки относительно оси 
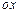и по ходу часовой стрелки относительно оси 
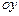, если смотреть в начало координат (в том и другом случаях растягиваются нижние волокна плиты).В прямоугольном треугольнике, кроме указанных перемещений, фиксируется поворот среднего сечения гипотенузы (точка 
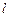на рис. 3) в перпендикулярной ей плоскости.
Матрица – строка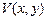 
прогибов от единичных смещений узловых точек определяется матричным произведением
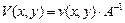. (19)
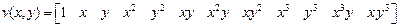
для прямоугольника,
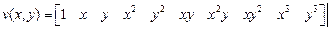
для треугольника.
Рис. 2 Рис. 3
Матрица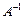 
строится подстановкой координат узлов, которым задаются перемещения, в 
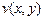и ее производные.
При решении задачи узлы обходятся в последовательности: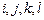 
. Сначала для каждого узла фиксируется угол поворота относительно оси 
- 
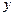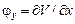, затем прогиб – 
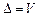и угол поворота относительно оси 
- 
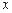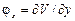. В треугольнике для узла 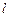фиксируется угол поворота в плоскости нормальной прямой 
-
= 
.
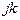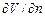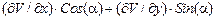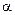– угол между прямыми 
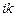и .
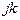Матрицы жесткостей равны
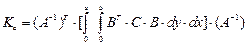(20)
для прямоугольника,
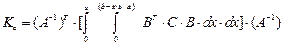(21)
для треугольника.
Матрица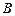 
– матрица деформаций, состоящая из трех строк. Компоненты первой строки 
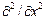, второй – 
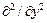, третьей – 
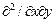от матрицы-строки .
.
,
.
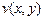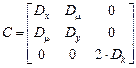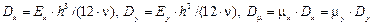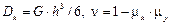Матрица реакций 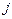‑того элемента от смещений узлов с единичными ускорениями (матрица эквивалентных масс) равна
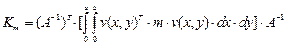(22)
для прямоугольника,
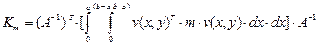(23)
для треугольного элемента.
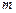– интенсивность распределенной массы.
Распределенная нагрузка заменяется узловой. Эквивалентная узловая нагрузка определяется из условия равенства возмож
ных работ узловых сил и заданной распределенной нагрузки.
В случае равномерно распределенной нагрузки узловые сосредоточенные силы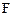 
для прямоугольного элемента равны произведению примыкающей к узлу площади на интенсивность нагрузки.
Для треугольного элемента они равны
,
.
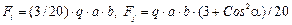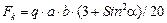Зависимость между изгибающими моментами и деформациями:
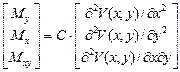. (24)
Изгибающие моменты являются линейными функциями координат и определяются в узловых точках. Крутящие моменты изменяются нелинейно и определяются в центре прямоугольного элемента и в точке 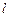треугольного элемента.
Вектор усилий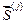 
равен
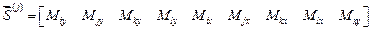
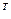(25)
для прямоугольного элемента и
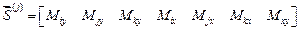
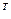( (26)
для треугольного элемента.
Первый индекс – номер узла, второй – ось, относительно которой действует момент. Знак плюс у изгибающих моментов показывает, что растянуты нижние волокна .
Вектор усилий, в случае узловой нагрузки и узловых сил инерции, определяется матричным произведением
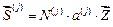. (27)
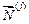– матрица распределенных усилий от единичных смещений узлов. Для прямоугольного элемента она определяется матрицей
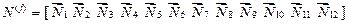. (28)
Для треугольника матрица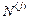 
равна матрице
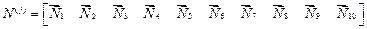.(29)
Векторы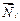 
( 
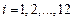) – векторы девятого порядка для прямоугольника и седьмого порядка для треугольника Их компоненты зависят от жесткостных характеристик и размеров элемента.
Компоненты 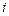того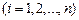 
столбца матрицы 
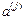записываются в последовательности: 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
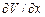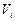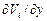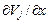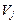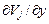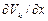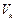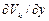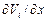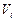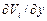для прямоугольника и в последовательности: 
, , , , , , , , , 
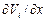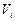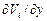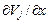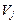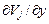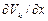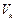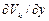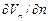для треугольного элемента.
Найденные усилия относятся к отдельным элементам. Они, как правило, имеют разные значения для элементов, примыкающих к одному и тому же узлу. Чтобы вычислить действитель
ный момент в узловой точке, нужно взять среднее значение от узловых моментов примыкающих к узлу элементов. Если элементы одинаковы, то сумма соответствующих моментов делится на число элементов, сходящихся в узле. Если же элементы имеют разную толщину и размеры, то действительный момент в точке определяется как сумма соответствующих моментов, умноженных на свои коэффициенты влияния, вычисляемые по формуле
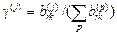. (30)
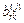– жесткость 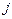‑того элемента узле 
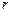, соответствующая его единичному повороту относительно оси 
.
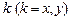Матрица преобразований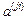 
от глобальной системы координат к локальной определяется произведением
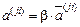, (31)
в котором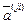 
– матрица перемещений 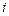‑того узла 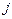‑того элемента в глобальной системе координат, а
.
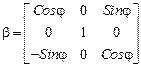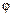– угол между глобальными и локальными осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала глобальной системы координат.
Допустим, что в глобальной системе координат перемещения 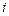‑того узла образуют матрицу
, 
.
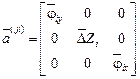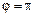Тогда
.
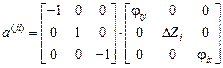Если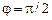 
,то
.
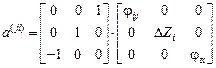В заключение следует отметить: рассмотренная аппроксимация прогибов дает достаточно точные результаты, хотя и допускает разрыв деформаций в углах поворота между смежными элементами. Решение получается приближенным. Степень приближения зависит от числа и вида элементов, на которые разбит конструктивный элемент, а также от градиента заданных возмущений.
1.4. Плоская задача теории упругости
Заданная система разбивается на прямоугольники и прямоугольные треугольники (рис. 4 ,рис. 5).
Каждый узел имеет три степени свободы: два линейных и одно угловое перемещение. Прямоугольная матрица 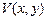определяется матричным произведением:
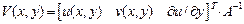, (32)
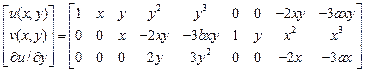
для треугольника и
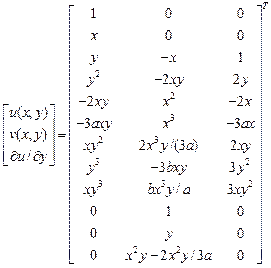
для прямоугольника.
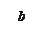
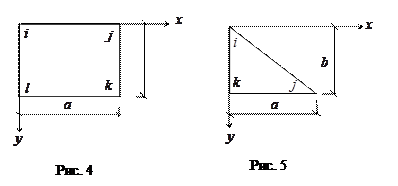
Матрица 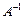строится подстановкой координат узлов, которым задаются перемещения, в 
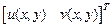и ее производных [ 
].
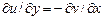При решении задачи узлы обходятся в последовательности
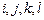. Сначала для каждого узла фиксируется 
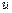, затем 
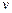и 
.
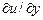Матрица жесткости равна матрице
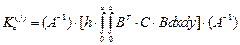(33)
для прямоугольника,
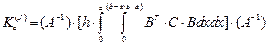(34)
для треугольника.
Матрица 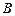– матрица деформаций, состоящая из трех строк. Компоненты первой строки 
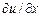, второй 
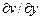, третьей – 
.
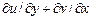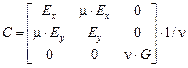, (35)
.
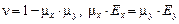Распределенная масса заменяется узловой. Узловые сосредоточенные массы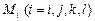 
для прямоугольника равны произведениям примыкающих к узлам площадям на интенсивность распределенной массы 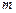. Узловые сосредоточенные массы для треугольника определяются по правилу рычага (массы распределяются между узлами обратно пропорционально длинам медиан) и равны:
,
,
,
,
,
.
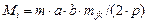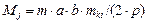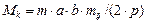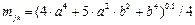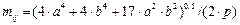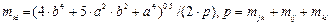Моменты инерции узловых масс условно принимаются равными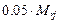 
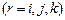, или нулю. В последнем случае угловым связям, накладываемым на систему, присваиваются последние порядковые номера.
Матрица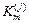 
– диагональная. Диагональные элементы записываются в последовательности:
, 
, 
,. 
.
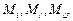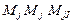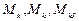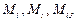Распределенная нагрузка заменяется узловой. Узловые силы определяются аналогично узловым массам.
Зависимость между усилиями и деформациями имеет вид:
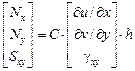. (36)
Нормальные усилия определяются для средин сторон четырех угольника, так как значения их больше чем в узлах. Сдвигающие усилия определяются в средней точке. В треугольнике усилия принимаются постоянными для всего элемента.
Вектор 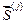усилий равен вектору
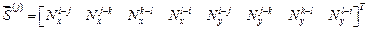(37)
для прямоугольного элемента (верхние индексы – стороны прямоугольника). Для треугольного элемента
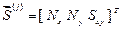. (38)
Вектор усилий, в случае узловой нагрузки и узловых сил инерции, определяется матричным произведением
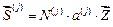. (39)
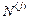– матрица распределенных усилий от единичных смещений узлов. Компоненты 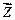записываются в последовательности: 
.
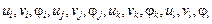Матрица преобразований 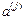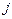‑того элемента в 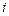‑том узле от глобальной системы координат к локальной определяется произведением
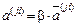, (40)
в котором 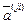матрица перемещений 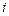‑того узла 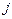-того элемента в глобальной системе координат, а
.
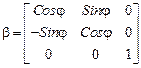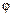– угол между глобальными и локальными осями. Он отсчитывается против хода часовой стрелки, если смотреть из начала координат глобальной системы.
1.5 Сооружения на упругом основании
Конструкция, в том числе и основание, разбивается на элементы. Элементам основания присваивается тип, одинаковый с типом расположенного на нем конструктивного элемента. Перемещения узлов основания принимаются равными перемещениям расположенного на нем конструктивного элемента. Влияние упругих сил основания заменяются эквивалентными узловыми силами исходя из равенства работ узловых и распределенных сил. В случае винклеровского основания давление со стороны основания на точку расположенного на нем элемента равно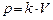 
. 
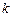–коэффициент упругого основания. Матрица узловых сил, в этом случае, равна матрице
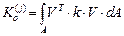(41)
и определяется по формулам для 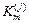подстановкой в них вместо интенсивности распределенной массы коэффициента .
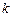Реакции основания от единичных смещений узлов равны
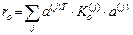. (42)
В уравнениях для определения основных неизвестных
= 
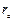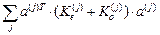(43).
В расчетной схеме на 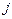‑тый элемент конструкции, расположенный на 
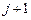элементе основания, действуют узловые силы, эквивалентные заданным возмущениям, концевые усилия, соответствующие деформированному состоянию элемента, и узловые силы, эквивалентные силам основания.
В стержневых системах узловые силы от заданных возмущений и упругого основания идентичны концевым усилиям, вызванных деформацией элемента. Поэтому вектор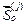 
концевых усилий стержневого элемента, расположенного на упругом основании, равен сумме:
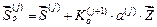, (44) где 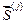определяется по (15)-(18). Из сопоставления точного решения с рассмотренным решением рекомендуется назначать длины отдельных элементов исходя из условия
.
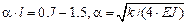В плитах эквивалентные узловые силы основания и заданных возмущений не идентичны концевым усилиям, вызванных деформацией элемента. Поэтому векторы усилий определяются произведением:
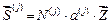. (45)
В расчетах на динамические возмущения масса основания присоединяется к массе элемента, расположенного на основании.
Элементы упругого основания, расположенные под одномерными конструктивными элементами не нумеруются. Элементам основания под двумерными конструктивными элементами присваивается порядковый номер, следующий за номером, расположенного на нем элемента конструкции.
1.6. Сокращение числа основных неизвестных
(Декомпозиция задачи)
Одним из способов декомпозиции является расчет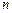 
раз кинематически неопределимой заданной системы с помощью 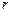раз кинематически неопределимой основной системы метода перемещений. Для перехода от системы с 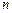основными неизвестными к системе с 
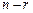неизвестными решается матричное уравнение
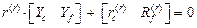(46)
и определяются матрицы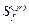 
- усилий от заданных возмущений и 
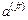- перемещений узлов от единичных смещений 
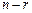связей 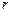кинематически неопределимой основной системы
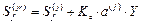(47)
в случае статических возмущений и
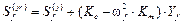(48)
в случае гармонических возмущений.
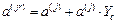. (49)
Матрица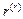 
- квадратная матрица порядка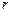
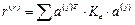- статический расчет,
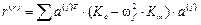- расчет на гармонические возмущения.
Матрица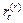 
прямоугольная матрица порядка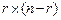 
.
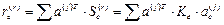
Матрица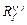 
- прямоугольная матрица порядка 
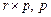- число заданных возмущений
.
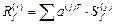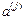- матрица перемещений узлов 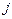- того элемента в кинематически определимой основной системе, 
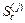- концевые усилия 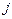- того элемента в кинематически определимой основной системе от единичных смещений 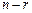связей, смещений, образующих матрицу 
. 
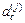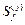- концевые усилия от заданных возмущений в кинематически определимой основной системе.
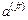- матрица перемещений узлов 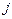- того элемента в 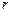раз кинематически неопределимой основной системе от единичных смещений 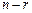введенных связей.
Матрицы усилий в заданной системе равны матрицам:
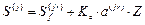(50)
от статических возмущений,
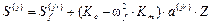, (51)
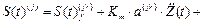
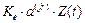(52)
от возмущений, изменяющихся во времени по произвольному закону,
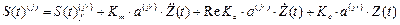(53) в диссипативных системах.
В элементах пятого – восьмого типа усилия вычисляются по (27) и (39) с заменой 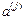на .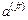
Матрицы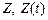 
определяются из уравнений (1), (2), (3), в которых при вычислении 
( = 
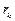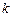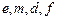) вместо 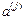подставляется .
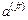1.7. Исходные данны е для решения задачи на ЭВМ
Подготовка исходных данных начинается с нумерации элементов и узлов. Узлы нумеруются в произвольном порядке. Первые порядковые номера присваиваются элементам первого типа, затем нумеруются элементы второго, третьего и т.д. типов. Элементу упругого основания под плитой присваивается порядковый номер, следующий за номером расположенного на нем конструктивного элемента. Элементы основания под одномерным конструктивным элементом не нумеруются.
После нумерации элементов и узлов составляются матрицы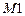 
, 
, 
( 
.
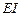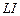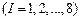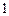. Матрица 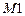. Матрица 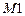– матрица-строка, состоящая из 20 компонент: 
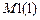– число неизвестных сил инерции в расчетах методом сил. В расчетах методом перемещений равняется нулю. 
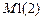– число основных неизвестных метода сил. В
расчетах методом перемещений равняется нулю.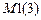 
– число перемещений узлов, принятых за основные неизвестные метода
перемещений.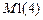 
– признак метода расчета. В расчетах методом перемещений = 2. 
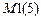– число одномерных элементов в состоянии стесненного кручения. 
, 
, 
, 
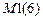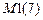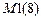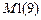– число элементов первого, второго, третьего и четвертого типов.
, 
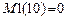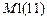– число связей от единичных смещений которых нужно определить перемещения по направлению основных неизвестных на первом этапе декомпозиции.
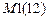– характеризует заданные возмущения. Если заданные возмущения статические - 
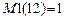, если гармонические и статические – 
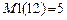, если система рассчитывается на статические возмущения и возмущения, изменяющиеся во времени по произвольному закону, – 
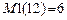, в расчетах на мгновенные импульсы – 
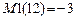.В расчетах диссипативных систем на установившиеся гармонические возмущения 
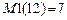. В расчетах на устойчивость 
. 
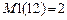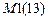– число независимых заданных возмущений.
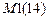– число сочетаний заданных возмущений. 
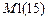– число заданных смещений связей в расчетах методом сил. В расчетах методом перемещений равно нулю, если осуществляется оптимизация конструкции, то М1(15) >0.
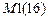– число статических возмущений. 
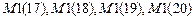– число элементов пятого, шестого, седьмого и восьмого типов.
2. Матрицы 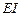– прямоугольные матрицы. Число их столбцов зависит от типа элементов и типа возмущений. Число строк равняется числу элементов данного типа.