Расчет статически и динамически
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО–
СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ (СИБСТРИН)
В.И. Роев
РАСЧЕТ СТАТИЧЕСКИ И ДИНАМИЧЕСКИ
НАГРУЖЕННЫХ СИСТЕМ
С ИСПОЛЬЗОВАНИЕМ ПРОГРАММНОГО
КОМПЛЕКСА DINAM
.
Учебное пособие
Новосибирск 2007
УДК 624.041.1
ББК 38.112
K 777
Роев В.И.
Расчет статически и динамически нагруженных систем с использованием программного комплекса DINAM: учеб. пособие;/
В.И.Роев; Новосиб. гос. архитектур.-строит. ун-т.- Новосибирск: НГАСУ, 2007, - 100 с.
ISBN 5-7795-0093-2
В учебном пособии рассмотрены вопросы расчета методом перемещений линейно деформируемых систем на статические и динамические возмущения. Пособие состоит из четырех частей. В первой части даны основные теоретические положения по составлению и решению систем разрешающих уравнений, определению усилий и перемещений в заданной системе на ЭВМ по программе DINAM. Во второй части рассмотрены конкретные примеры расчета стержневых систем. В третьей – примеры определения усилий и перемещений в системах из тонких плит. В четвертой – примеры расчета плоско напряженных пластин.
Печатается по решению издательско-библиотечного совета
НГАСУ
Рецензенты:
- И.И.Крылов, канд. техн. наук, профессор кафедры
металлических и деревянных конструкций НГАСУ;
Г.Б.Лебедев, канд. техн. наук, доцент кафедры
строительной механики НГАСУ;
Н.Н. Пантелеев, д-р технических наук, профессор
кафедры железобетонных конструкций НГАСУ.
ISBN 5-7795-0093-2 Роев В.И., 2007-01-17
НГАСУ(Сибстрин) 2007
ОГЛАВЛЕНИЕ
Введение ……………………………………………. 3
1. Основные теоретические положения 6
1.1. Основные неизвестные. Система канонических
уравнений…………………………………... 6
1.2. Стержневые системы…………………………… 13
1.3. Тонкие плиты…………………………………… 22
1.4. Плоская задача теории упругости…………….. 28
1.5. Сооружения на упругом основании…………… 33
1.6. Сокращение числа основных неизвестных…… 35
1.7.Исходные данные для решения задачи на ЭВМ
по программе ‘DINAM’……………………….. 37
1.8.Ввод исходных данных………………………… 47
1.9.Результаты расчета……………………………… 48
2. Кинематически неопределимые стержневые
системы…………………………………………… 4 9
2.1.Основная система. Исходные данные………… 49
2.2.Статические возмущения………………… …… 50
Определение усилий от заданной нагрузки
с учетом деформации сдвига……………………. 50
Определение усилий от смещения связей и
неточностей изготовления………………………..55
Определение усилий по деформированной схеме.56
Определение критического параметра нагрузки.. 58
Определение усилий в балке на упругом
основании………………………………………….. 61
2.3.Динамические возмущения……………………….63
Определение усилий от статических и гармони-
ческих возмущений………………………………..63
Определение усилий от возмущений, изменяю-
щихся во времени по произвольному закону……68
Определение усилий от мгновенного импульса
с учетом деформации сдвига…………………….73
Определение усилий в диссипативной
системе…………………………………………….76
3. Тонкие плиты……………………………………. 80
3.1. Тонкие плиты. Основная система.Исходные…
данные …………………………………………….81
Расчет тонкой плиты на статические ..
и гармонические возмущения………………… 82
Расчет плиты на винклеовском основании на
статические и гармнические возмущения………87
4. Плоская задача теории упругости……………… 93
4.1. Основная система. Исходные данные…………..93
Расчет стенки на статические возмущения……..94
Расчет стенки на статические и гармонические..
возмущения………………………………… 96
Заключение.....................................................................100
Литератута……………………………………… 104
Введение
Реальное сооружение рассматривается как система, состоя-щая из идеально упругих линейно деформируемых элементов.
Элементами могут быть стержни, ортотропные тонкие плиты и плоско напряженные ортотропные пластины.
Задача определения напряженно-деформированного состония указанных систем решается методом конечных элементов в форме метода перемещений. Стержень плоской системы представляется изгибаемым и растянутым (сжатым) элементами. Стержень пространственной – тремя элементами: двумя изгибаемыми в главных плоскостях элементами и элементом, рабо-
тающим на растяжение и кручение. Тонкие плиты представляются системой прямоугольных и треугольных элементов, соеде-
ненных между собой в узлах. Плоско напряженные пластины за-
даются системой прямоугольных и треугольных элементов.
Напряженно-деформированное состояние стержня основной системы от смещений введенных связей и заданных возмущений определяется обычным порядком с учетом и без учета деформации сдвига и по деформированной схеме при заданных
продольных силах.
Поверхность изгиба прямоугольного элемента плиты от смещений узлов задается неполным бикубическим полиномом
двенадцатого порядка и полиномом с десятью параметрами для
треугольного элемента.
Перемещения плоско напряженных прямоугольных и тре-
угольных элементов определяются полиномами двенадцатого и
десятого порядков соответственно.
Основные неизвестные- перемещения узлов в расчетах на статические возмущения определяются из системы n линейных
неоднородных алгебраических уравнений. Коэффициенты при основных неизвестных и свободные члены определяются по теореме о работе концевых усилий: реакция I – той связи в k
состоянии равна работе концевых усилий k-того состояния на
перемещениях, вызванных единичным смещением i -той связи.
В случае динамических возмущений составляется и решается система n линейных дифференциальных уравнений второго прядка. Их общее решение находится обычным порядком. Произвольные постоянные частного решения на i –том интервале определяются из двух систем линейных неоднородных алгебра- ических уравнений порядка 2n , свободные члены которых соответствуют заданным возмущениям.
Точность расчета систем из тонких плит и плосконапряженных пластин зависит от числа и вида элементов, представляющих заданную систему. Напряженно-деформированное состо-
яние стержневых систем определяется точно.
Решение перечисленных выше задач осуществляется на ЭВМ по программе DINAM.
Исходные данные – компоненты матриц M1, EI, LI (I = 1,2,3,4,5,6,7,8), K.
M1- матрица строка характеризует основную систему,метод
расчета, число основных неизвестных, число и тип элементов основной системы, характер и число заданных возмущений.
Компоненты j-той строки матрицы EI – линейные размеры и жесткости j – того элемента, интенсивность массы и момента инерции массы, коэффициент внутреннего трения.
Матрицы LI состоят из блоков. Число блоков равно числу элементов I-того типа. Число столбцов в блоке равно n+r. r – число заданных возмущений. Компоненты i-того столбца - перемещения концевых сечений от единичного смещения i-той связи, компоненты n+1,…,n+r - концевые усилия от заданных
возмущений.
Матрица K – матрица сочетаний заданных возмущений. Число строк равно числу заданных возмущений. Число столбцов – числу сочетаний заданных возмущений.
После ввода матриц LI запрашивается масштабная жесткость, масштабная масса и круговая частота заданных гармонических возмущений.
На печать выдаются исходные данные,матрица коэффициентов при основных неизвестных, матрица свободных членов и матрицы концевых усилий в элементах заданной системы.
Программа позволяет определять критический параметр заданной нагрузки. Решает систему 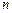 линейных алгебраических уравнений, вычисляет собственные числа и векторы квадратной матрицы
линейных алгебраических уравнений, вычисляет собственные числа и векторы квадратной матрицы 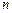 ‑го порядка
‑го порядка
Одномерные конструктивные элементы в расчетах представляются совокупностью прямых стержней постоянной жесткости; двумерные конструктивные элементы – совокупностью прямоугольников и прямоугольных треугольников.
Изгибаемый стержень, жестко соединенный с узлами, относится к элементам первого типа; стержень, соединенный с другими элементами одним концом жестко, а другим шарнирно, относится к элементам второго типа; изгибаемый стержень, шарнирно соединенный с другими, и растянутый (сжатый) стержень – относятся к элементам третьего типа; узел и стержень, деформацией которых можно пренебречь, – элементы четвертого типа. Стержень в состоянии стесненного кручения – элемент первого типа.
Стержень пространственной системы в расчетах представляется тремя элементами: двумя изгибаемыми и элементом, работающим на кручение и растяжение (сжатие ).
Треугольный элемент плиты – элемент пятого типа, треугольный элемент плоской задачи – элемент шестого типа; прямоугольный элемент плиты – элемент седьмого типа, прямоугольный элемент плоской задачи – элемент восьмого типа.
Пластинчатые системы, произвольно расположенные в пространстве, в расчетах представляются элементами пятого, шестого, седьмого и восьмого типов.
Задача определения напряженно-деформированного состояния стержневых систем решается точно. Напряженно-деформированные состояния систем из двумерных элементов определяется приближенно.
1. Основные теоретические положения
1.1. Основные неизвестные. Система канонических
уравнений
За основные неизвестные принимаются угловые и линейные перемещения узлов. Вектор 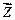 основных неизвестных в статических расчетах определяется из уравнения
основных неизвестных в статических расчетах определяется из уравнения
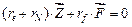 . (1)
. (1)
В динамических расчетах консервативных систем для определения 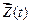 составляется и решается уравнение
составляется и решается уравнение



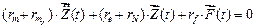 . (2)
. (2)
Основные неизвестные диссипативных систем определяются из уравнения
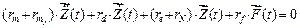 . (3)
. (3)
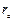 – матрица жесткостей основной системы – матрица реакций веденных связей от их единичных смещений. Её компоненты зависят от жесткостей элементов заданной системы
– матрица жесткостей основной системы – матрица реакций веденных связей от их единичных смещений. Её компоненты зависят от жесткостей элементов заданной системы
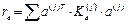 .
.
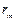 – матрица эквивалентных масс– матрица реакций введенных связей от их смещений с единичными ускорениями . Ее компоненты зависят от масс элементов системы
– матрица эквивалентных масс– матрица реакций введенных связей от их смещений с единичными ускорениями . Ее компоненты зависят от масс элементов системы
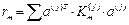 .
.
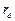 – матрица реакций введенных связей от их смещений с единичными скоростями. Ее компоненты функции коэффициентов внутреннего трения и демпфирования
– матрица реакций введенных связей от их смещений с единичными скоростями. Ее компоненты функции коэффициентов внутреннего трения и демпфирования
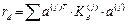 .
.
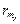 – матрица реакций введенных связей от их смещений с единичными ускорениями. Ее компоненты зависят от моментов инерции масс элементов системы
– матрица реакций введенных связей от их смещений с единичными ускорениями. Ее компоненты зависят от моментов инерции масс элементов системы
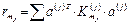 .
.
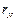 – матрица реакций введенных связей от их единичных смещений. Ее компоненты – функции продольных сил
– матрица реакций введенных связей от их единичных смещений. Ее компоненты – функции продольных сил
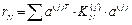 .
.
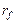 – прямоугольная матрица реакций введенных связей от единичных значений заданных возмущений
– прямоугольная матрица реакций введенных связей от единичных значений заданных возмущений
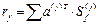 .
.
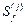 – матрица концевых усилий в элементах основной системы от единичных значений заданных возмущений.
– матрица концевых усилий в элементах основной системы от единичных значений заданных возмущений.
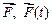 – векторы заданных возмущений.
– векторы заданных возмущений.
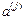 – прямоугольная матрица перемещений концевых сечений (узлов) j‑того элемента в локальной системе координат от единичных смещений связей, введенных при выборе основной системы. Число ее столбцов равно числу связей, введенных при выборе основной системы; число строк зависит от типа элемента.
– прямоугольная матрица перемещений концевых сечений (узлов) j‑того элемента в локальной системе координат от единичных смещений связей, введенных при выборе основной системы. Число ее столбцов равно числу связей, введенных при выборе основной системы; число строк зависит от типа элемента.
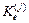 ,
, 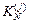 – матрицы жесткостей j-того элемента основной системы от единичных смещений его концевых сечений (узлов),
– матрицы жесткостей j-того элемента основной системы от единичных смещений его концевых сечений (узлов),
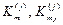 – от смещений узлов с единичными ускорениями,
– от смещений узлов с единичными ускорениями,
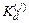 – от смещений узлов с единичными скоростями.
– от смещений узлов с единичными скоростями.
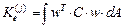 ,
,
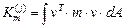 ,
,
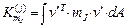
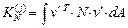 .
.
w – матрица преобразований перемещений в деформации,
v – матрица перемещений, C – матрица жесткостей, 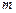 – интенсивность массы,
– интенсивность массы, 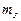 интенсивность момента инерции массы,
интенсивность момента инерции массы, 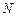 – продольная сила. В дальнейшем продольные силы считаются заданными.
– продольная сила. В дальнейшем продольные силы считаются заданными.
Компоненты 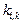 матрицы
матрицы 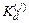 принимаются равными
принимаются равными
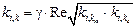
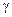 – коэффициент внутреннего трения,
– коэффициент внутреннего трения,
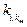 ,
, 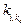 – компоненты матриц
– компоненты матриц 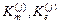 соответственно.
соответственно.
Для элементов четвертого типа
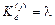 ,
,
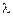 – коэффициент демпфирования.
– коэффициент демпфирования.
Общие решения уравнений (2), (3) находятся обычным порядком. Для отыскания частных решений время действия заданных возмущений разбивается на интервалы длиной 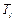 так, чтобы функции
так, чтобы функции 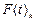 – компоненты вектора
– компоненты вектора 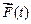 на протяжении интервала не имели ни переломов, ни перегибов, ни скачков. Вектор
на протяжении интервала не имели ни переломов, ни перегибов, ни скачков. Вектор 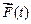 на
на 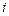 – том интервале аппроксимируется матричным произведением
– том интервале аппроксимируется матричным произведением
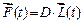 , (4)
, (4)
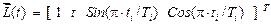
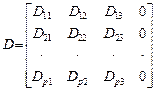 .
.
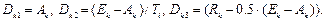
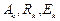 – значения компоненты
– значения компоненты 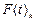 вектора
вектора 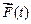 в начале, средине и конце интервала
в начале, средине и конце интервала 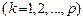 .
.
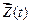 в этом случае можно задать произведением
в этом случае можно задать произведением
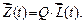 (5)
(5)
в котором 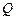 – матрица порядка
– матрица порядка 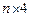 постоянных коэффициентов.
постоянных коэффициентов.
Подставляя (5) в (3), получим:
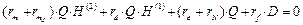 (6)
(6)
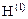 =
= 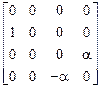 ,
, 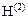 =
= 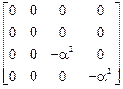 ,
, 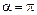 /T
/T  .
.
Уравнение (6) – система двух матричных уравнений,
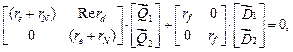 (7)
(7)
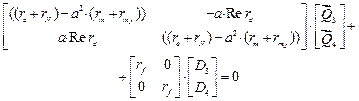
В случае гармонических возмущений 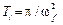 , компоненты двух первых столбцов матрицы
, компоненты двух первых столбцов матрицы 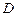 равны нулям, компоненты третьего столбца равны амплитудным значениям заданных возмущений. Поэтому
равны нулям, компоненты третьего столбца равны амплитудным значениям заданных возмущений. Поэтому
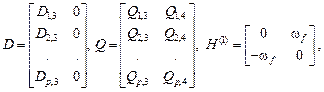
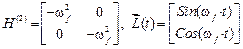 .
.
Уравнение (6) трансформируется в уравнение
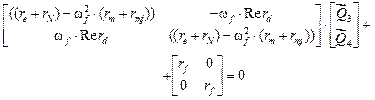 (8)
(8)
Для консервативных систем (6) трансформируется в уравнение
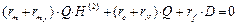 , (9)
, (9) 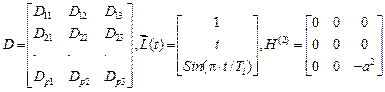 ,
,
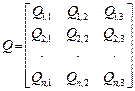 .
.
Компоненты 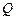 определяются из уравнений
определяются из уравнений
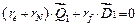 ,
,
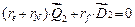 ,
,
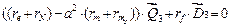 .
.
Амплитудные значения 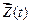 в случае гармонических возмущений консервативных систем определяются из уравнения
в случае гармонических возмущений консервативных систем определяются из уравнения
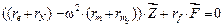 . (10)
. (10)
Стационарные колебания диссипативных систем при гармонических возмущениях описываются частным решением (3). За интервал принимается 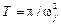 . Компоненты двух первых столбцов матрицы
. Компоненты двух первых столбцов матрицы 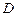 равны нулям. Компоненты третьего столбца равняются амплитудным значениям
равны нулям. Компоненты третьего столбца равняются амплитудным значениям 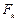 заданных возмущений.
заданных возмущений. 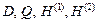 преобразуются в матрицы
преобразуются в матрицы
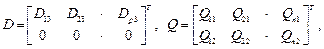
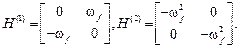
Вектор 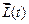 трансформируется в вектор
трансформируется в вектор
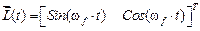 .
.
Уравнение (6) превращается в систему уравнений
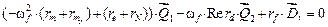 ,
, 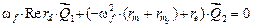 .
.
Компоненты 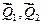 равны соответственно компонентам первого и второго столбцов матрицы
равны соответственно компонентам первого и второго столбцов матрицы 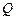 . Компоненты
. Компоненты 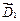 равны компонентам первого столбца матрицы
равны компонентам первого столбца матрицы 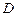 .
.
Расчет на мгновенный импульс состоит из двух этапов. На первом этапе решается уравнение
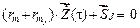 , (11)
, (11)
в котором 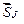 вектор заданных мгновенных импульсов.
вектор заданных мгновенных импульсов.
На втором этапе заданная система рассчитывается на свободные колебания с начальными условиями :
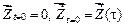 .
.
1.2 . Стержневые системы
Изгиб, растяжение, кручение.
Изгибаемый стержень, жестко соединенный с узлами
Деформированное состояние стержня определяется углами поворота 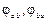 концевых сечений и их линейными смещениями
концевых сечений и их линейными смещениями 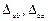 по нормали к его оси. Положительные направления перемещений и концевых усилий показаны на рис. 1.
по нормали к его оси. Положительные направления перемещений и концевых усилий показаны на рис. 1.
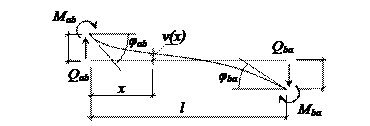
Рис. 1
Матрица 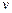 перемещений поперечных сечений стержня с защемленными концами определяется матричным произведением
перемещений поперечных сечений стержня с защемленными концами определяется матричным произведением
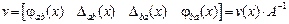 . (12)
. (12)
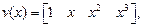
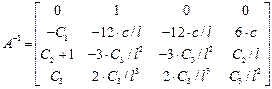 ,
,
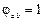
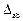 =1
=1 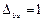
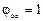

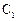 =1 – 6*c,
=1 – 6*c, 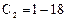 *c,
*c, 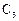 =1- 12*c
=1- 12*c
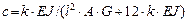
для элементов сплошного сечения.
Для элементов сквозного сечения
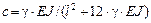 .
.
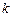 –коэффициент формы поперечного сечения,
–коэффициент формы поперечного сечения, 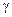 –относитель-ный угол сдвига.Если деформация сдвига не учитывается c =0.
–относитель-ный угол сдвига.Если деформация сдвига не учитывается c =0.
Изгибаемый стержень с защемленным концом 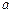 и шарнирно опертым концом
и шарнирно опертым концом 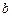 .
.
Деформированное состояние определяется углом поворота сечения 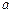 и перемещениями
и перемещениями 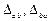 концов стержня по нормали к его оси.
концов стержня по нормали к его оси.
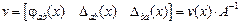 , (13)
, (13)
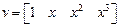
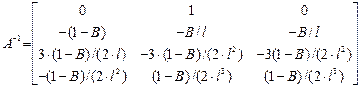 .
.
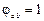
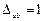
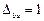
Для элементов сплошного сечения
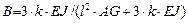 .
.
Для элементов сквозного сечения
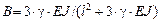 .
.
Коэффициенты 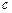 и
и 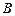 учитывают влияние деформации сдвига. Если деформация сдвига не учитывается
учитывают влияние деформации сдвига. Если деформация сдвига не учитывается 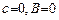 .
.
Матрица 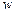 преобразований перемещений в деформации
преобразований перемещений в деформации
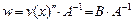 . (14)
. (14)
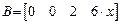 .
.
Матрицы 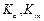 ,
, 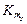 ,
, 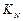 равны:
равны:
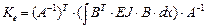 ,
,
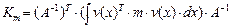 ,
,
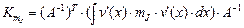 ,
,
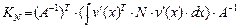 .
.
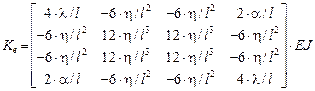
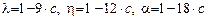 ,
,
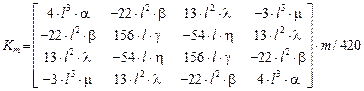 ,
,
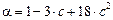 ,
, 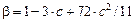 ,
,
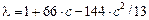 ,
, 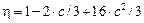 ,
,
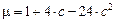 ,
,
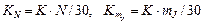 ,
,
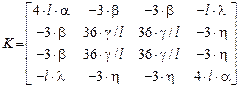 ,
,
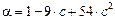 ,
, 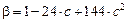 ,
,
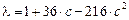 ,
, 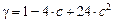 ,
,
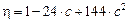 ,
,
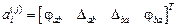 .
.
для элементов первого типа.
Для элементов второго типа:
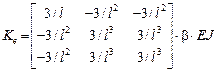 ,
, 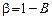 ,
,
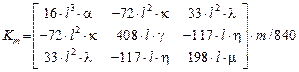 ,
,
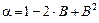 ,
, 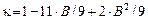 ,
,
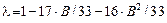 ,
, 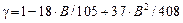 ,
, 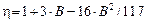 ,
, 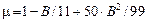 ,
,
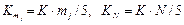 ,
,
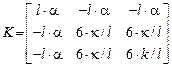 ,
,
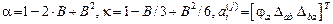 .
.
Для растянутых (сжатых) элементов третьего типа
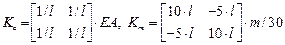 ,
,
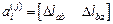
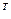 .
.
Положительное направление усилий и перемещений соответствует удлинению стержня.
Для изгибаемых элементов третьего типа
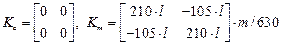 ,
,
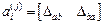
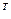 .
.
Положительное направление 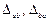 соответствует повороту стержня по часовой стрелке.
соответствует повороту стержня по часовой стрелке.
Для скручиваемых элементов третьего типа
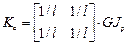 ,
, 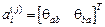 .
.
Положительным 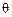 соответствует поворот сечения относительно оси
соответствует поворот сечения относительно оси 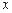 по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали.
по ходу часовой стрелки, если смотреть на сечение со стороны внешней нормали.
Для элементов четвертого типа
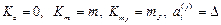 .
.
Концевые усилия образуют векторы:
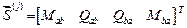 – элементы первого типа,
– элементы первого типа,
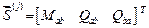 – элементы второго типа,
– элементы второго типа,
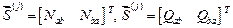 ,
, 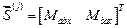 . - элементы третьего типа.
. - элементы третьего типа.
В заданной системе указанные векторы равны
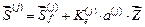 (15)
(15)
от статических возмущений;
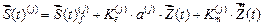 (16)
(16)
от динамических возмущений, изменяющихся во времени по произвольному закону;
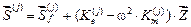 (17)
(17)
амплитудные значения усилий в консервативных системах от гармонических возмущений;
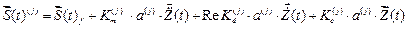
(18)
в диссипативных системах в случае установившихся гармонических колебаний.








