№34. Диагональ AC основания прямой призмы ABCDA 1 B 1 C 1 D1 равна 6 см, а высота призмы равна см. Найдите угол наклона диагонали A 1 C к плоскости основания.

Дата: 2025-06-15; Просмотры: 8

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

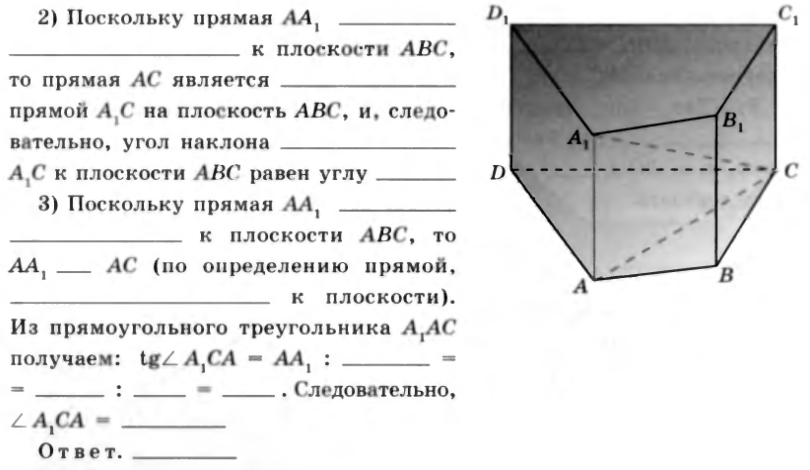Решение. 1) Из определения прямой призмы следует, что ее боковое ребро ______________ _______________________ к плоскости _______________________ и равно высоте __________, т.е. AA₁ = 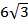см.

2)Поскольку прямая AA₁ ____________________________ к плоскости ABC, то прямая AC является ____________________ прямой A ₁ C на плоскость ABC, и, следовательно, угол наклона ________________ A ₁ C к плоскости ABC равен углу ___________

3)Поскольку прямая AA₁ ________________________ к плоскости ABC, то AA₁________ AC (по определению прямой, ___________________________ к плоскости). Из прямоугольного треугольника A ₁ AC получаем: 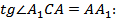_________=_________:________=_______. Следовательно, __________

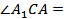Ответ. __________

2.Пирамида. Усеченная пирамида.

№35. Основание пирамиды – прямоугольник ABCD, AB = 18 м, BC = 10 м, высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 м. Найдите площадь полной поверхности пирамиды.

Решение. 1) Площадь полной поверхности пирамиды вычисляется по формуле 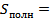__________+__________. Так как основание пирамиды - _________________________ со сторонами 10 м и __________, то _____*_____=_________ ( .

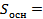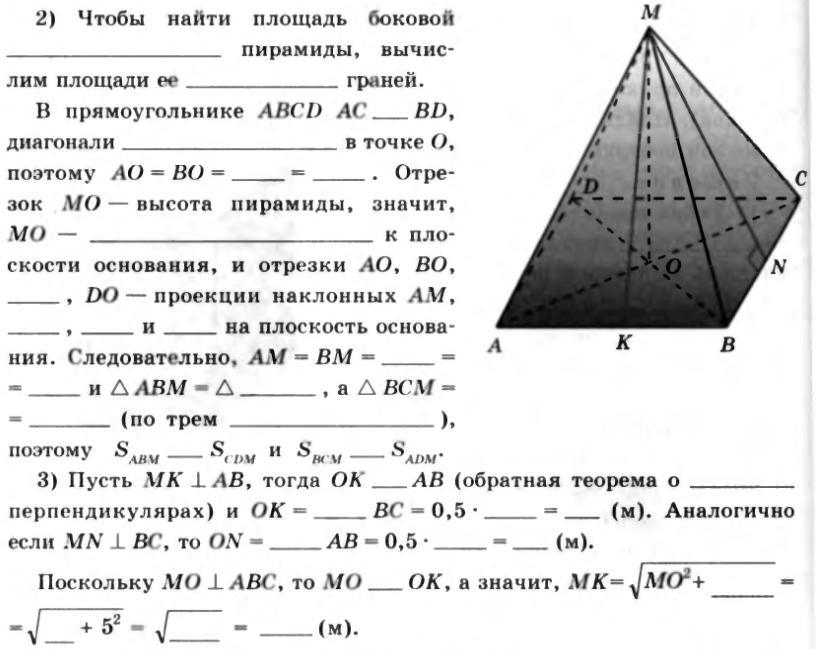2)Чтобы найти площадь боковой ____________________ пирамиды, вычислим площади ее _______________ граней.

В прямоугольнике ABCD AC ____BD, диагонали ___________________ в точке O, поэтому AO = BO =_____=_____. Отрезок MO – высота пирамиды, значит, MO - ____________________ к плоскости основания, и отрезки AO , BO, _____, DO – проекция наклонных AM, _____, _____, _____ и _____ на плоскость основания. Следовательно, AM = BM = _____ = _____ и 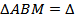_____, а 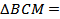_______ (по трем ____________________ ), поэтому .

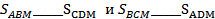3)Пусть 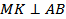, тогда OK_____AB (обратная теорема о __________ перпендикулярах) и OK = _____ BC = 0,5*_____=_____ (м). Аналогично если 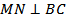, то ON = _____AB = 0,5*_____ = _____ (м).

Поскольку 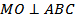, то MO_____OK, а значит, 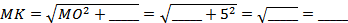(м).

Аналогично 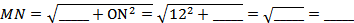(м).

Итак, , 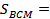_______________________ _________________. Отсюда получаем: =__________ ( ), .

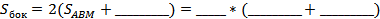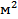Ответ. _________________________

№36. Основание пирамиды – параллелограмм со сторонами 6 см и 8 см, высота пирамиды равна 12 см, а все боковые ребра равны между собой. Найдите длину бокового ребра.

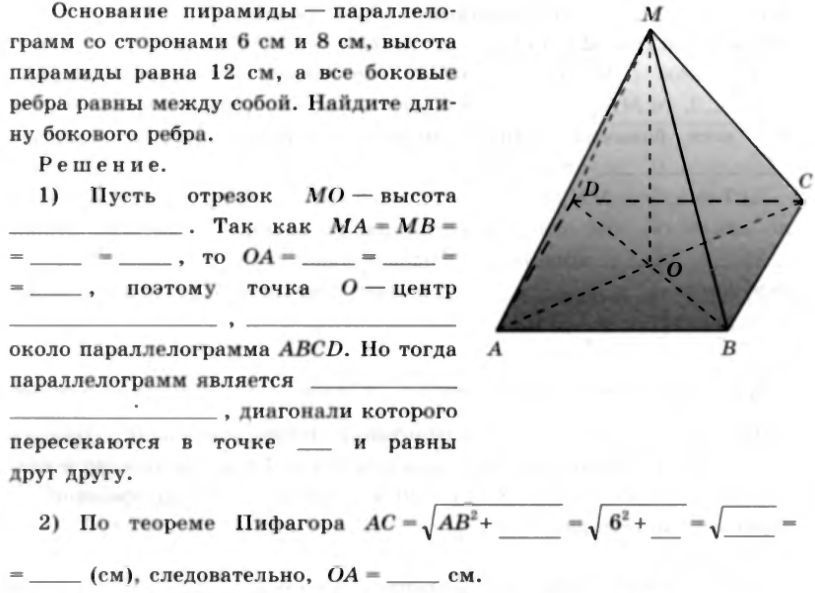Решение. 1) Пусть отрезок MO – высота _______________. Так как MA=MB=_____=_____, то OA =_____=_____=_____, поэтому точка O – центр _______________, _______________ около параллелограмма является ______________________________, диагонали которого пересекаются в точке _____ и равны друг другу.

2)По теореме Пифагора 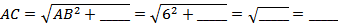(см), следовательно, OA = _____ см.

3) 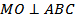, поэтому MO _____OA. В треугольнике AMO 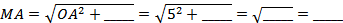(см).

Ответ. _________

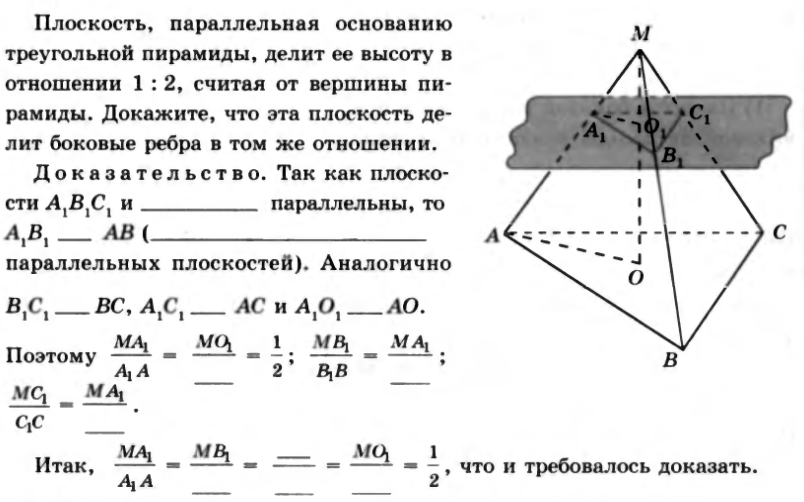№37. Плоскость параллельная основанию треугольной пирамиды, делит ее высоту в отношении 1:2, считая от вершины пирамиды. Докажите, что эта плоскость делит боковые ребра в том же отношении.

Доказательство. Так как плоскости A ₁ B ₁ C₁ и __________ параллельны, то A ₁ B₁_____AB (____________________ параллельных плоскостей). Аналогично B ₁ C₁_____BC, A ₁ C₁_____AC и A ₁ O₁ _____AO. Поэтому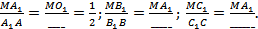

Итак, 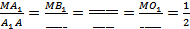, что и требовалось доказать.

3.Правильные многогранники.

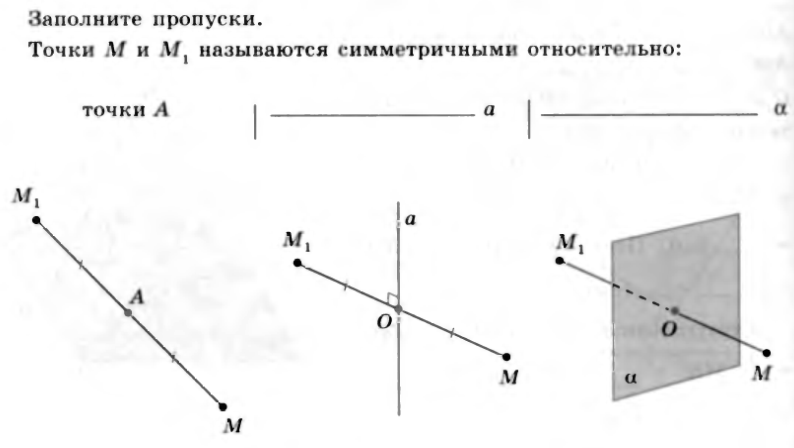
№38. Заполните пропуски.

Точки M и M₁ называются симметричными относительно:

точки A _________________ a __________________ a

№39. Заполните пропуски:

а) Точка называется ____________________ симметрии фигуры, если _______________ точка фигуры _________________________ относительно нее некоторой точке той же _____________

б) Прямая называется осью ____________________ фигуры, если каждая точка фигуры симметрична _________________________ нее некоторой _______________ той же фигуры.

в) Плоскость называется ____________________ симметрии фигуры, если _______________ _________________________________________________________________ относительно нее _____________________________________________ фигуры.

№40. Заполните пропуски в определении правильного многогранника:

Выпуклый ________________________ называется правильным, если __________ его грани - _________________________ многоугольники, и в ___________________ его _____________ сходится одно и то же число _______________

№41. Докажите, что куб является правильным многогранником.

Доказательство. Проверим, обладает ли куб всеми признаками правильного ____________________, указанными в определении.

1)Куб ____________________ выпуклым многогранником.

2) Каждая грань куба - _______________, т.е. _____________ _________ многоугольник, и все грани _______________ между собой.

3) В ____________________ вершине куба сходится ________________________ число ребер, а именно _____ ребра.

Итак, у куба ______________ все признаки, указанные в определении ______________ многогранника. Следовательно, куб ____________________ правильным __________________, что и требовалось доказать.

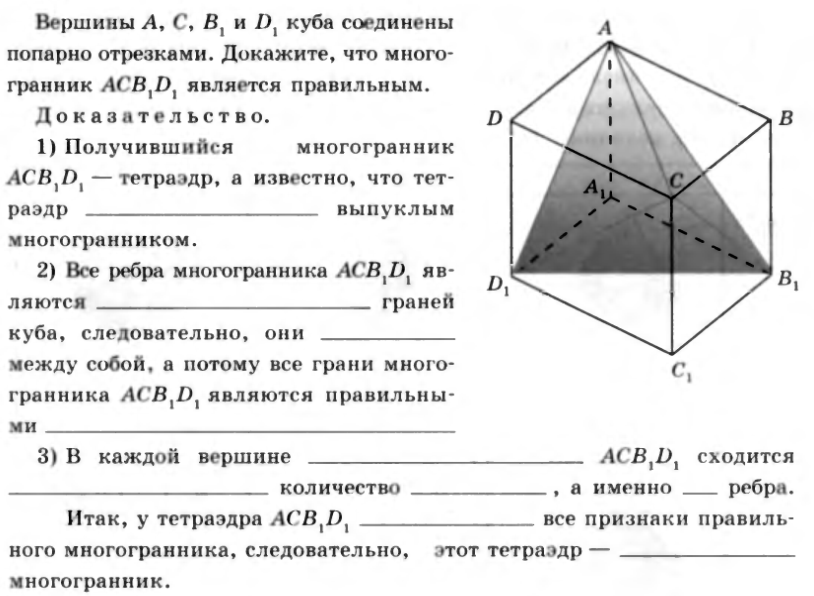
№42. Вершины A , C , B ₁ и D₁ куба соединены попарно отрезками. Докажите, что многогранник ACB ₁ D₁ является правильным.

Доказательство. 1) Получившийся многогранник ACB ₁ D₁ – тетраэдр, а известно, что тетраэдр ______________________ выпуклым многогранником.

2)Все ребра многогранника ACB ₁ D₁ являются __________________ граней куба, следовательно, они ________________ между собой, а потому все грани многогранника ACB ₁ D₁ являются правильными ________________________________

3)В каждой вершине ____________________ ACB ₁ D₁ сходится ____________________ количество ________________, а именно ____ ребра.

Итак, у тетраэдра ACB ₁ D₁ _______________ все признаки правильного многогранника, следовательно, этот тетраэдр - ____________________ многогранник.

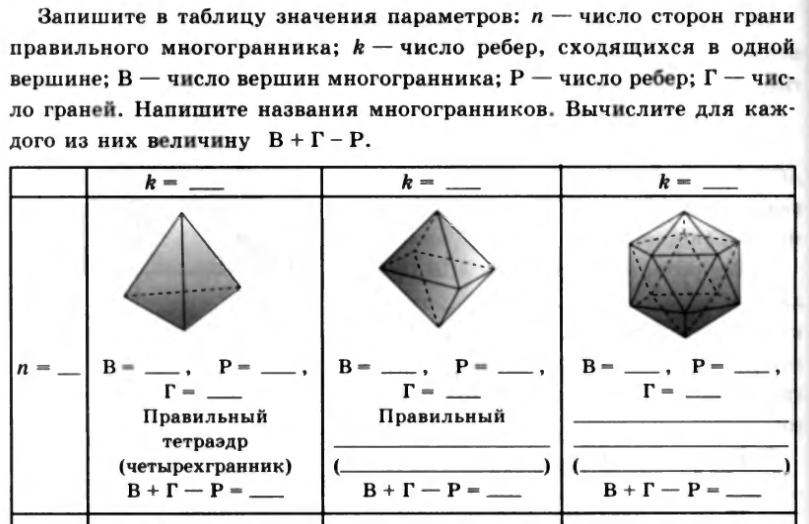
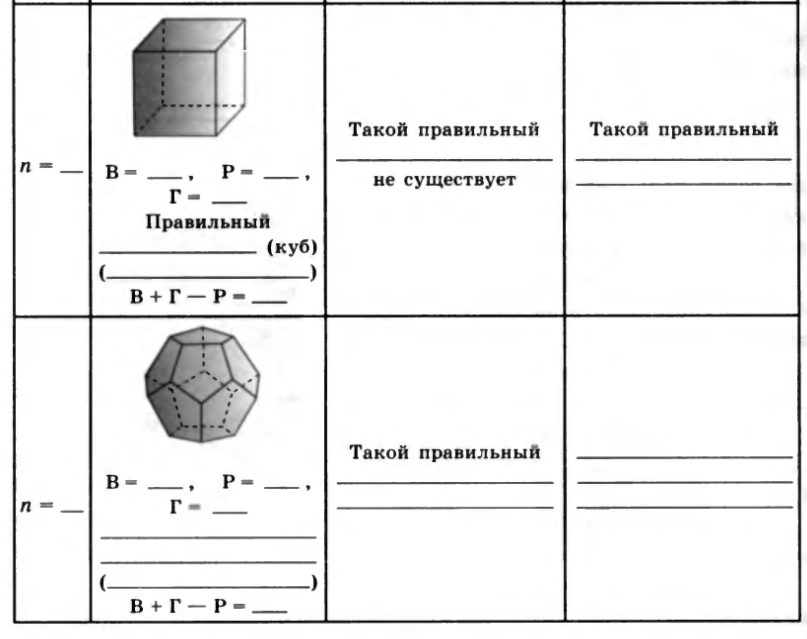
№43. Запишите в таблицу значения параметров: n – число сторон грани правильного многогранника; k – число ребер, сходящихся в одной вершине; B – число вершин многогранника; P – число ребер; Г – число граней. Напишите названия многогранников. Вычислите для каждого из них величину В +Г – Р.

4.Поверхность тел вращения. Цилиндр.

№44. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагона­лью и образующей цилиндра равен 60⁰. Найдите:

а) высоту цилиндра;

б) радиус цилиндра;

в) площадь боковой поверхности ци­линдра.

Решение.

Осевое сечение цилиндра представля­ет собой _ , сторо­ны ВС и AD которого являются _ цилиндра, а две другие стороны – оснований цилиндра. По условию задачи BD = _ см. 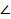DBC = _

а) Высота цилиндра равна его , а BС = BD *соs =

= * = (см), т.е. высота равна см.

б) Радиус цилиндра — это основания цилиндра: 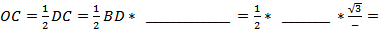(см).

в) Площадь боковой _ цилиндра равна произведению _ окружности цилиндра на цилиндра, т.е. = .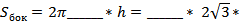

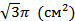Ответ.

а) см; б) см; в) см².

№45. Площадь боковой поверхности цилиндра равна S. Найдите площадь осевого сечения цилиндра. (Задача 538 учебника.)

Решение. Пусть h – высота цилиндра, r – его радиус. По условию задачи 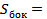_____, т.е.

2πr____ = S. (1)

Осевым сечением цилиндра является _________________________ со сторонами 2r и _____. Поэтому площадь осевого сечения равна _____ * h. Учитывая равенство (1), получаем .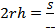

Ответ. __________

№46. Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке.

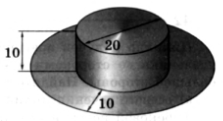Решение.

Если дно шляпы опустить на плоскость ее полей, то получим круг радиуса r = ____ см.

Площадь боковой поверхности цилиндрической части вычисляем по формуле 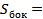___ ______r ₁ h, где r₁ = ____________ см, _________ = 10 см. Следовательно, 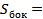_______10*10 = ________ (см²).

Итак, 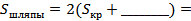____________см².

Ответ. ____________ см².

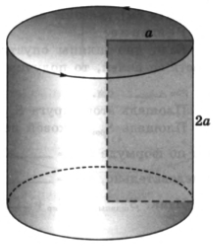№47. Цилиндр получен вращением прямоугольника со сторонами a и 2a вокруг большей стороны. Найдите площадь:

а) осевого сечения цилиндра;

б) боковой поверхности цилиндра.

Решение. Пусть r – радиус цилиндра, h – его высота. По условию r = ____, h = ____

а)

б)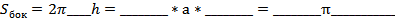

Ответ. а) ________; б) __________

5.Конус. Усеченный конус.

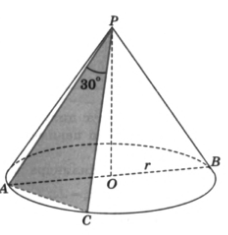№48. Радиус основания конуса равен 2 м, а осевое сечение - прямоугольный тре­угольник. Найдите площадь сечения, проведенного через две образующие, угол между которыми равен 30⁰.

Решение. По условию задачи треугольник АРВ- ____________________, а так как PA = ____, то 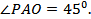В прямоугольном треугольнике PAO катет 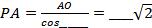м.

Пусть 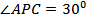, тогда сечение, проведенное через образующие PA и ____, является ____ _______________________________ треугольником, в котором PC = ______ = 2 ______ м. Поэтому 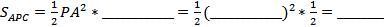(м²).

Ответ. ________

№49. Осевое сечение конуса — треугольник со стороной 8 см и прилежа­щим углом 120°. Найдите площадь полной поверхности конуса.

Решение. Осевым сечением конуса является ____________________ треуголь­ник. По условию задачи один из углов этого треугольника равен __________, сле­довательно, это угол, противолежащий _______________ стороне треугольника, а потому боковые стороны треугольника равны _____ см, т. е. образующая l конуса равна ______ см. Из прямоугольного треугольника РОА находим радиус основания конуса: 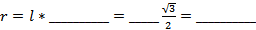(см). Таким образом, 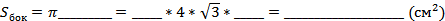, (см²).

Ответ. ____________________

№50. В трапеции ABCD A = 90°, 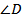=45⁰. ВС = 4 см, CD = 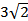см. Вычислите пло­щади боковой и полной поверхностей усеченного конуса, образованного вра­щением данной трапеции вокруг сторо­ны АВ. (Задача 571 учебника.)

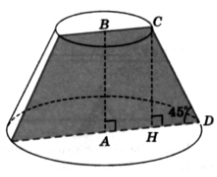Решение. При вращении данной трапеции получается _____________________ конус.

1)Проведем 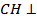___________. Тогда 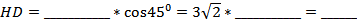см, AD = AH +______ = ______ + HD = ______ см.

2) (см²).

3) (см²).

Ответ. ____________ см² и __________________

6. Шар и сфера.

№51. Точки A и B лежат на сфере с центром 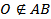, а точка M лежит на отрезке AB. Докажите, что:

А) если M – середина отрезка AB, то ;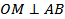

Б) если 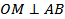, то M – середина отрезка AB.

(задача 573 учебника)

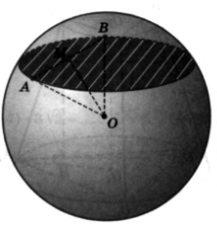Доказательство. а) Пусть точка M – середина отрезка AB , R – радиус сферы. 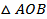равнобедренный, так как ________________ = R, поэтому медиана OM является также ________ ________________, т.е. ________________AB.

Б) Пусть . Треугольник AOB равнобедренный, и OM – его высота по ___________, следовательно, OM – его ____________________, т.е. M - _________________________

№52. Шар радиуса 17 см пересечен плоскостью, находящейся на расстоянии 8 см от центра. Найдите площадь сечения.

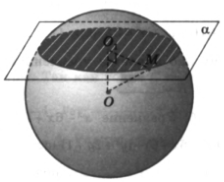Решение. Пусть точка O – центр шара радиуса R = 17 см, α – секущая плоскость и 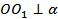. По условию задачи расстояние OO₁ от центра шара до секущей плоскости меньше радиуса шара, поэтому сечением шара плоскостью α является ____________, площадь которого 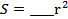, где ____ - радиус сечения. Возьмем точку M на линии пересечения сферы и плоскости α, тогда треугольник OO ₁ M ________________ ( , OM = R = ____________, OO₁ = ____ см), откуда находим: O ₁ M = r =________, ____________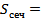

Ответ. ____________ см².