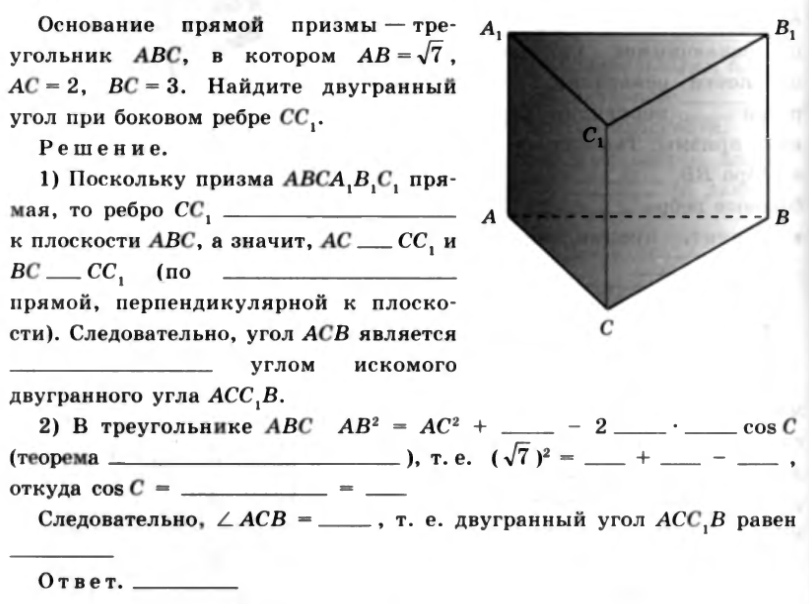
Геометрические тела и поверхности.
1.Тело и его поверхность. Многогранники. Призма. Параллелепипед и его свойства.
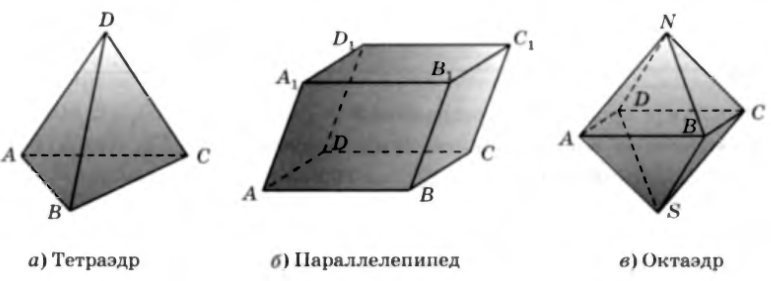
№28. Сколько граней, ребер, вершин и диагоналей у каждого из изображенных на рисунке многогранников?
Решение.
а)Тетраэдр DABC составлен из ___________ граней. Он имеет ___________ ребер и _______ вершины. Диагональю многогранника называется ______________, соединяющий две _______ _______, не принадлежащие _____________________. У тетраэдра любые две вершины _______ _____________________ одной грани, следовательно, у него ______________ диагоналей.
б) ________________________________ ABCDA 1 B 1 C 1 D1 составлен из ____________ граней. Он имеет __________ ребер, _______ вершин и _______ диагонали (AC1, _________________).
в) __________________________ NABCDS имеет ___________________________________ _____________ и _____________ диагонали (AC, ________________ ).
№29. Заполните пропуски в предположении:
В выпуклом многограннике сумма всех __________________ углов при __________________ его вершине __________________ 3600.
№30. Какой из данных многогранников является призмой?
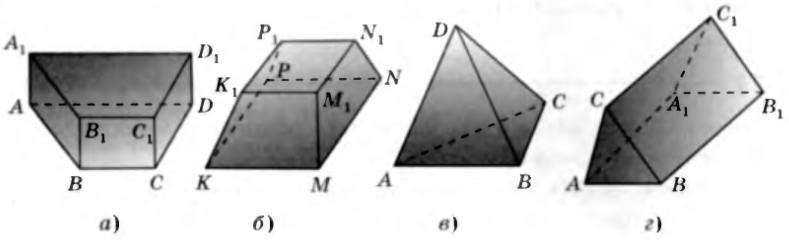
Решение. а) Грани ABCD и A 1 B 1 C 1 D1 многогранника ____________________________ равны и расположены в параллельных ______________________________. Остальные ________ грани – параллелограммы. Следовательно, __________________________ ABCDA 1 B 1 C 1 D1 __________ ____________ призмой.
б) Грань KK 1 M 1 M многогранника ________________________ не является _______________ ________________________. Следовательно, этот многогранник _________________________ призмой.
в) У многогранника ABCD нет граней, расположенных в ______________________________ плоскостях. Следовательно, этот многогранник _________________________________ призмой.
г) Грани ABC и A 1 B 1 C 1 ________________________ ABCA 1 B 1 C1 – равные ________________, расположенные в ________________________ плоскостях. Остальные ________ грани являются ________________________________________. Следовательно, многогранник ABCA 1 B 1 C1 _____ _______________________________ призмой.
№31. Высота призмы равна 5 см. Чему равно расстояние между плоскостями оснований призмы?
Решение. Основания призмы расположены в _____________________________ плоскостях, а расстоянием между параллельными плоскостями называется ____________________ от произвольной _____________________ одной из параллельных ___________________ до другой плоскости.
Расстоянием от данной точки до плоскости называется длина ____________________, проведенного из этой ____________ к данной _________________
Поскольку высота призмы называется ______________________, проведенный из какой-нибудь точки одного _______________________ к плоскости другого _________________, то длина высоты и есть искомое _________________________ между плоскостями оснований ________________
Ответ. ____ см.
№32.
Докажите, что все боковые грани прямой призмы являются прямоугольниками.
Доказательство.
1) Прямой призмой называется ____________ , боковые ребра которой ______________ к основаниям. Но если прямая перпендикулярна к плоскости, то по определению она _____________ к любой прямой, лежащей в этой _________________. Следовательно, боковые ребра прямой призмы ________________________________ к сторонам основания.
2)Каждая боковая грань призмы является _________________________,
а параллелограмм, смежные стороны которого взаимно перпендикулярны, является ____________________. Следовательно, все боковые грани прямой призмы — ____, что__ и требовалось доказать.
№33.