Найдите расстояние между основаниями наклонных, если проекция наклонной MA равна см.

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Решение. 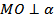, поэтому 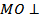_______ и 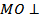_______. 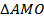прямоугольный и равнобедренный: 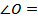______, 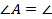____=______, AO = ______, следовательно, MO = _____, AM = _______. 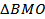прямоугольный: 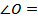_____, 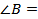____, MO = ____, поэтому MB=2___= ____ см.

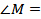прямоугольный: _______, AM = ________, BM = ________, поэтому AB = _________________ = ______________= ________ см.

Ответ. ________ см.

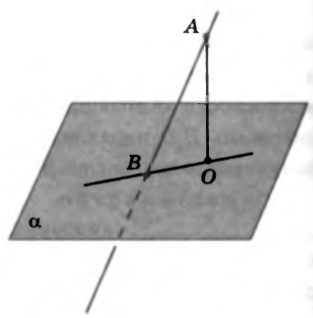№22. Через точку A, удаленную от плоскости α на расстояние 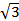см, проведена прямая, пересекающая плоскость α в точке B. Найдите угол между прямой AB и плоскостью α, если AB = 2 см.

Решение. Пусть отрезок AO – перпендикуляр к плоскости α. Тогда AO = ____________, прямая OB – проекция ____________ ________________________, а угол между прямой AB и плоскостью α равен 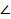________. Из прямоугольного треугольника AOB находим: 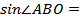________=________, следовательно, ________

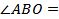Ответ. ________

№23. В прямоугольном треугольнике ABC 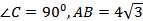см. Точка P не лежит в плоскости ABC и удалена от каждой вершины треугольника на расстояние 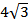см. Найдите угол между прямой PC и плоскостью ABC.

Решение. Пусть PO – перпендикуляр к плоскости ABC. Поскольку отрезки PA , PB , PC – равные наклонные, проведенные из _______________ к _________________________________, то их проекции тоже ____________, т.е. OA = _________=_________, а потому точка O – центр окружности, ______________________________________________________________________. Следовательно, точка O – середина ________________________. Так как AB = ____________, то 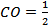______=______ см.

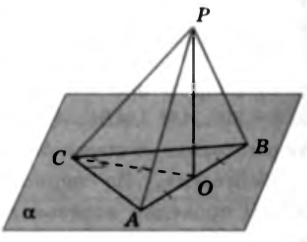Искомый угол 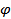между прямой ______ и плоскостью ______ есть угол между ________________________________ ___________________________________, т.е. 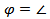________. 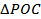прямоугольный, так как _____________________, PC = ____________, CO = __________ см, поэтому 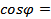________ = __________ = _________. Отсюда получаем, что ______

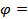Ответ. ______

8.Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей.

№24. К плоскости равнобедренного прямоугольного треугольника ABC с гипотенузой 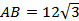см проведен перпендикуляр DC, равный 18 см. Найдите угол между плоскостями DAB и CAB.

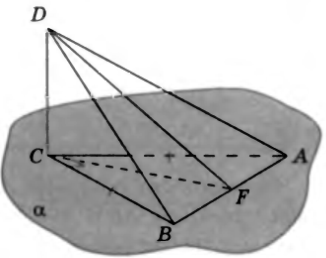Решение. Треугольники ABC и ADB равнобедренные: 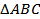_______________________, а в 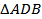DA = _______, так как эти стороны - ______________________________ _____________ __________________________. Поэтому медианы CF и DF этих треугольников, проведенные из вершин C и D к общему основанию ________, являются __________________, и, следовательно, 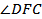- линейный угол _____________________________________________, а значит, угол между плоскостями DAB и CAB равен 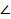______. 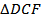прямоугольный, DC=_____, 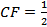______=______ см и поэтому 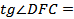______ = ______ = ______, откуда ____

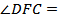Ответ. ______

№25. Катет AC прямоугольного треугольника ABC с прямым углом C лежит в плоскости α, а угол между плоскостями α и ABC равен 60⁰. Найдите расстояние от точки B до плоскости α, если AC = 5 см, AB = 13 см (задача 172 учебника).

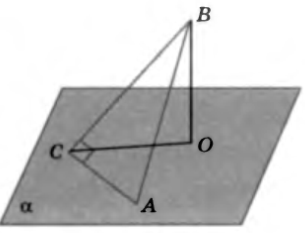Решение. Проведем перпендикуляр BO к плоскости α. Отрезок BC – наклонная к _________ ________________________, отрезок OC – проекция наклонной ______ на __________________, а прямая AC, лежащая в плоскости α, перпендикулярна к наклонной BC. Следовательно, согласно _____________ 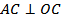________________________________________________ _____________, . Таким образом, 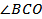- линейный угол двугранного угла между плоскостями α и ABC, и, значит, ________

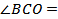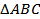прямоугольный: 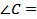______, AC = ________, AB = _________, поэтому BC = _________

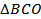прямоугольный: 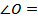______, 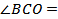______, BC = _________, следовательно BO = _____________ см = ____________ см = ______ см.

Ответ. ______ см.

№26. Через сторону AD ромба ABCD проведена плоскость ADM так, что двугранный угол BADM равен 60⁰. Найдите сторону ромба, если 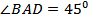и расстояние от точки B до плоскости ADM равно 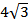(задача 176 учебника).

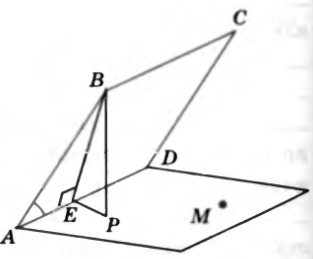Решение. Проведем перпендикуляр BP к плоскости ADM. Искомое расстояние от точки B до плоскости ADM равно BP. Проведем высоту ромба BE . Тогда получим, что из точки B к плоскости ADM проведены перпендикуляр ______ и наклонная ______

Следовательно, отрезок PE – проекция _________________ __________ на ________________

Прямая AD, лежащая в плоскости ADM, перпендикулярна к наклонной BE, а потому, согласно 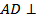_____________________ _____________________________________________________, ______, и 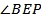- линейный угол ________________________________________________, т.е. ________

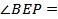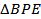прямоугольный, так как _______________________________, причем 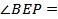_____ , BP = _________, поэтому BE = _________________________ = _________________ = _________

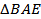прямоугольный: 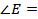_______, 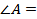______, BE = __________, следовательно, AB = ________________ = __________

Ответ. ____________

№27. Найдите измерения прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ если его диагональ В D₁ =24 см и составляет с плоскостью грани DAA₁, угол в 45⁰ , а с ребром DD ₁, — угол в 60⁰ .

Решени е. Все грани прямоугольного параллелепипеда — ____________________, поэтому BA _______ , ВА ______, и, следовательно, BA DAA₁. Прямая BD₁ пересекает плоскость DAA₁ в точке ________ , а прямая AD₁ — проекция____ на эту плоскость, поэтому 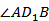=____. Из прямоугольного треугольника 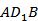, в котором 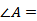_________, D ₁ B = __________ и 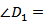______, находим: AB = AD₁ = _______=________ см. Из прямоугольного треугольника BD ₁ D, в котором 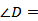_______, BD₁= ____, 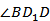=___ по условию, получаем 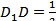______= ______ см. Из треугольника AD ₁ D, в котором 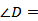______, AD₁=__________, DD₁=______, находим: AD = ______ см.

Ответ. _______________