№13. На рисунке . Докажите, что линия пересечения плоскостей AFC и BMC параллельна прямым AF и BM.
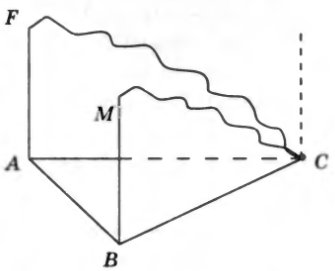 Доказательство. Так как
Доказательство. Так как 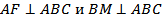 , то AF║________, и, следовательно, AF║BMC по _______________________________________ _________________ . Плоскость AFC проходит через прямую AF, параллельную плоскости ________, и пересекает эту плоскость. Следовательно, линия пересечения плоскостей _______________ параллельна прямой _______. А так как AF║BM, то по ___________________________________ ___________________________ прямая BM также параллельна _______________________________________________________ ____________________.
, то AF║________, и, следовательно, AF║BMC по _______________________________________ _________________ . Плоскость AFC проходит через прямую AF, параллельную плоскости ________, и пересекает эту плоскость. Следовательно, линия пересечения плоскостей _______________ параллельна прямой _______. А так как AF║BM, то по ___________________________________ ___________________________ прямая BM также параллельна _______________________________________________________ ____________________.
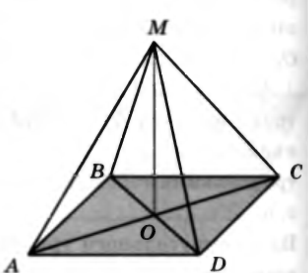 №14. Четырехугольник ABCD – квадрат, O – точка пересечения его диагоналей,
№14. Четырехугольник ABCD – квадрат, O – точка пересечения его диагоналей, 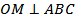 . Докажите, что:
. Докажите, что:
а) 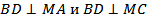 ;
;
б) 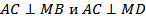 .
.
Доказательство. Четырехугольник ABCD – квадрат, поэтому 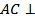 ________. По условию
________. По условию 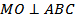 , следовательно,
, следовательно, 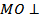 ________ и
________ и 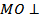 ________
________
а) Рассмотрим плоскость AMC. Прямая BD перпендикулярна к двум пересекающимся прямым ________________ этой плоскости, следовательно по ____________________________ ________________________________________________ BD 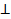 _______, а потому прямая BD перпендикулярна к любой прямой, лежащей в этой плоскости, в частности BD
_______, а потому прямая BD перпендикулярна к любой прямой, лежащей в этой плоскости, в частности BD 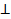 ______ и BD
______ и BD  _____
_____
б) Рассмотрим плоскость BMD. ___________________________________________________ _________________________________________________________________________________ _________________________________________________________________________________ _________________________________________________________________________________
________________________________________________________________________________
№15. В тетраэдре MABC AB = AC, MB = MC. Докажите, что 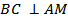 .
.
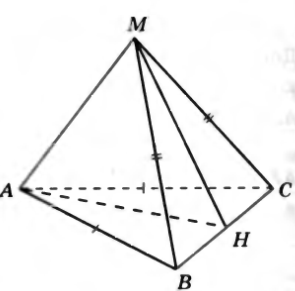 Доказательство. По условию треугольники BAC и BMC - _______________________ с общим ___________________________, поэтому их медианы AH и MH, проведенные к _____________ __________________, являются ________________________, т.е.
Доказательство. По условию треугольники BAC и BMC - _______________________ с общим ___________________________, поэтому их медианы AH и MH, проведенные к _____________ __________________, являются ________________________, т.е. 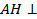 ______ и _____________
______ и _____________
Рассмотрим плоскость AMH. Так как 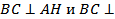 ______, то по _________________________________________________ ______________
______, то по _________________________________________________ ______________ 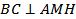 , а потому прямая BC перпендикулярна к любой _______________________________________________ _______, в частности
, а потому прямая BC перпендикулярна к любой _______________________________________________ _______, в частности 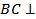 _______
_______
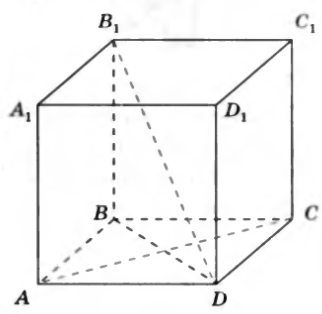 №16. Дан куб ABCDA 1 B 1 C 1 D 1. Докажите, что диагональ куба B 1 D перпендикулярна к диагонали AC его основания.
№16. Дан куб ABCDA 1 B 1 C 1 D 1. Докажите, что диагональ куба B 1 D перпендикулярна к диагонали AC его основания.
Доказательство. Так как грани AA 1 B 1 B и BB 1 C 1 C – квадраты, то 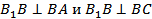 . Следовательно,
. Следовательно, 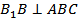 по ______________________________________________________. Рассмотрим плоскость
по ______________________________________________________. Рассмотрим плоскость 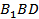 . Поскольку
. Поскольку 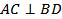 , так как _______________________________, и
, так как _______________________________, и 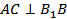 , так как _______________________, то
, так как _______________________, то 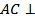 __________ по _____________________________________________________ __________________________, а потому
__________ по _____________________________________________________ __________________________, а потому 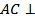 _____________
_____________
6.Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
№17. Концы отрезка отстоят от плоскости α на расстояниях 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости α (задача 142 учебника).
Решение. Рассмотрим два случая:
1) концы отрезка находятся по одну сторону от плоскости α;
2) концы отрезка находятся по разные стороны от плоскости α.
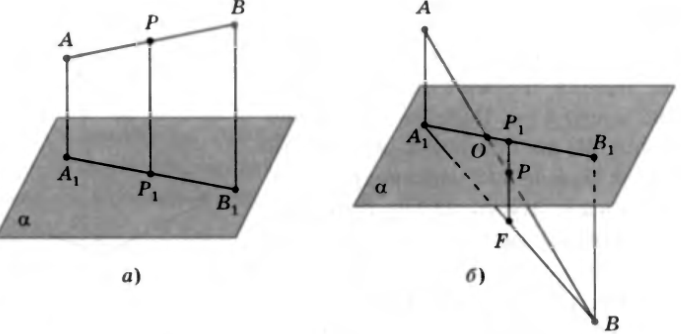
1) Пусть отрезок AB расположен по одну сторону от плоскости α (см.рис.a), 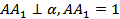 см,
см, 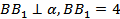 см. Так как
см. Так как 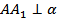 и
и 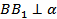 , то
, то 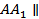 ______, и поэтому четырехугольник A 1 ABB 1 - ____________. Проведем в ней среднюю линию PP 1, тогда PP 1║_______, PP 1║_______, и так как
______, и поэтому четырехугольник A 1 ABB 1 - ____________. Проведем в ней среднюю линию PP 1, тогда PP 1║_______, PP 1║_______, и так как 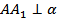 , то и PP 1
, то и PP 1 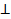 _______. Следовательно, длина отрезка PP 1 и есть искомое расстояние от середины отрезка AB до плоскости α,
_______. Следовательно, длина отрезка PP 1 и есть искомое расстояние от середины отрезка AB до плоскости α, 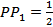 ____________________ = ____________________=________ см.
____________________ = ____________________=________ см.
2) Пусть концы отрезка AB расположены по разные стороны от плоскости α (см.рис.б) и пусть AA 1 и BB1 – перпендикулярны к плоскости α, 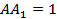 см,
см, 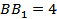 см. Так как
см. Так как 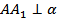 и
и 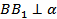 , то
, то 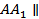 ______, и прямые AA 1 , BB 1 , A 1 B 1 лежат в одной ____________________. Проведем через точку P – середину отрезка AB – прямую, параллельную B1B. Тогда по _____ _____________________________________________ точки P1 и F пересечения этой прямой с прямыми A 1 B 1 и A 1 B будут серединами отрезков ________ и _________, а отрезки P 1 F и PF – средними _______________________________________________________________________. P1P = P1F - ________ = ____________________=________ см.
______, и прямые AA 1 , BB 1 , A 1 B 1 лежат в одной ____________________. Проведем через точку P – середину отрезка AB – прямую, параллельную B1B. Тогда по _____ _____________________________________________ точки P1 и F пересечения этой прямой с прямыми A 1 B 1 и A 1 B будут серединами отрезков ________ и _________, а отрезки P 1 F и PF – средними _______________________________________________________________________. P1P = P1F - ________ = ____________________=________ см.
Ответ. _________ см или ________ см.
№18. Расстояние от точки M до каждой вершин правильного треугольника ABC равно 4 см. Найдите расстояние от точки M до плоскости ABC, если AB = 6 см (задача 143 учебника).
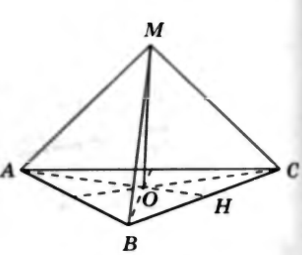 Решение. Пусть MO – перпендикуляр к плоскости ABC, тогда расстояние от точки M до плоскости α равно ______. Так как
Решение. Пусть MO – перпендикуляр к плоскости ABC, тогда расстояние от точки M до плоскости α равно ______. Так как 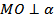 , то
, то 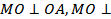 ______,
______, 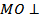 _____.
_____. 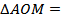 =_______________=_______________ по _____________ _____________________________________________________ _____________________________________________________ ___________________________________________________ ____ _________________________________, следовательно, OA = OB = OC, т.е. точка O равноудалена от ______________________________ ___________________ и, значит, является центром этого треугольника. Поэтому AO = ________ = ____________________= ____________(см), и из прямоугольного треугольника AMO находим: MO = _______________ = _______________(см) = ______ см.
=_______________=_______________ по _____________ _____________________________________________________ _____________________________________________________ ___________________________________________________ ____ _________________________________, следовательно, OA = OB = OC, т.е. точка O равноудалена от ______________________________ ___________________ и, значит, является центром этого треугольника. Поэтому AO = ________ = ____________________= ____________(см), и из прямоугольного треугольника AMO находим: MO = _______________ = _______________(см) = ______ см.
Ответ. ______ см.
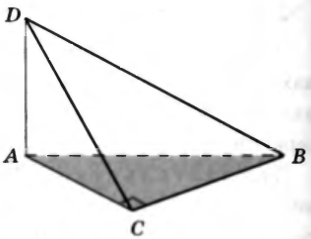 №19. Через вершину A прямоугольного треугольника ABC с прямым углом C проведена прямая AD, перпендикулярная к плоскости треугольника. Докажите, что треугольник CBD прямоугольный (задача 145 а учебника).
№19. Через вершину A прямоугольного треугольника ABC с прямым углом C проведена прямая AD, перпендикулярная к плоскости треугольника. Докажите, что треугольник CBD прямоугольный (задача 145 а учебника).
Доказательство. Из точки D к плоскости ABC проведены перпендикуляр _____ и наклонная ______. Прямая BC лежит в плоскости ABC и перпендикулярна к проекции ______ наклонной ______ на эту плоскость, поэтому, согласно ______________________________________________________________, 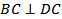 , т.е. треугольник CBD ____________________________________
, т.е. треугольник CBD ____________________________________
№20. Дан параллелепипед ABCDA 1 B 1 C 1 D 1 основанием которого является ромб ABCD, а боковое ребро перпендикулярно к плоскости основания. Докажите, что диагональ B 1 D параллелепипеда перпендикулярна к диагонали AC его основания.
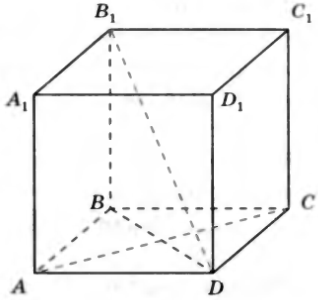 Доказательство.
Доказательство. 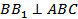 _______________________, диагональ AC лежит в плоскости ABC,
_______________________, диагональ AC лежит в плоскости ABC, 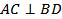 , так как _________________________________________________ __________________________________. Следовательно, согласно теореме ___________________________,
, так как _________________________________________________ __________________________________. Следовательно, согласно теореме ___________________________, 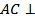 _________
_________
7.Угол между прямой и плоскостью.
№21. Из точки M к плоскости α проведены перпендикуляр MO и две наклонные MA и MB, которые образуют со своими проекциями на эту плоскость 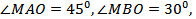 угол между наклонными равен 900.
угол между наклонными равен 900.








