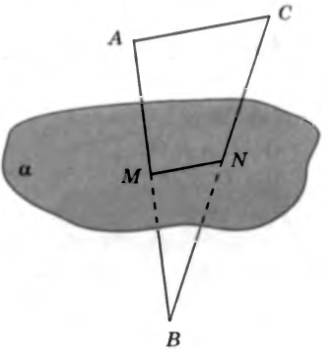
№5. Сторона AB треугольника ABC лежит в плоскости , а вершина , точки M и N – середины сторон AC и BC. Докажите, что прямая .

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Доказательство. Так как MN – средняя линия ________________, то 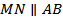, а потому, согласно _________________________________, .

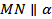№6. Сторона AC треугольника ABC параллельна плоскости 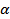, а стороны AB и BC пересекаются с этой плоскостью в точках M и N. Докажите что треугольники ABC и MBN подобны (задача 26 учебника).

Доказательство. На рисунке плоскость ABC проходит через прямую ________, параллельную плоскости 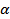, и пересекает ее по ________________, следовательно, __________, а потому ___________.

3.Признак скрещивающихся прямых.

Теорема (признак скрещивающихся прямых). Если одна из двух прямых лежит в некоторой плоскости, а другая прямая _____________________________, в точке, _________ ____________________________________, то эти прямые скрещивающиеся.

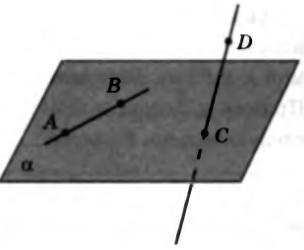Дано: прямая AB лежит в плоскости 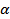, прямая CD пересекает плоскость , .

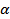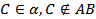Доказать: прямые AB и СВ - _______________________________

Доказательство. Допустим, что прямые AB и CD не ____________________. Тогда они будут лежать в некоторой ________________ β. Так как в этой плоскости будут лежать прямая AB и C, то плоскость β совпадает с ________________________, а значит, прямая CD _______________ __________________________________________, что противоречит _______________________ . Теорема доказана.

Задачи:

№7. На рисунке изображен куб. Докажите, что прямые:

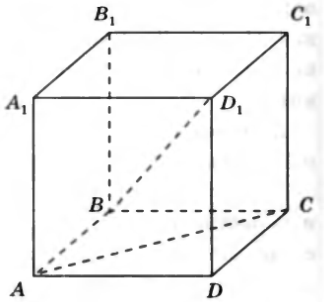а) AA₁ и B ₁ C ₁;

б) A ₁ D ₁ и DC;

в) AC и BD ₁ -

являются скрещивающимися.

Доказательство.

А) Прямая B ₁ C ₁ лежит в плоскости B ₁ C ₁ D ₁, а прямая AA ₁ пересекает эту плоскость __________________ , причем 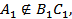так как ________________________ , поэтому, согласно ____________________________________, прямые AA ₁ и 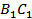являются _________________________________.

б) ________________________________________________________________________________ __________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

в) ________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

__________________________________________________________________________________

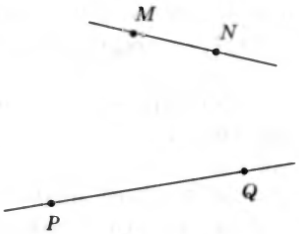
№8. Прямые MN и PQ скрещивающиеся. Докажите, что прямые MQ и NP также скрещивающиеся.

Доказательство. Допустим, что прямые MQ и NP не ______ ______________________________. Тогда они лежат в некоторой плоскости β. Так как 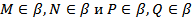, то, согласно ____________________, прямые ___________ также будут ______________________ . Но это противоречит условию. Значит, прямые MQ и NP _____________________ .

4.Взаимное расположение двух плоскостей. Признак параллельности двух плоскостей.

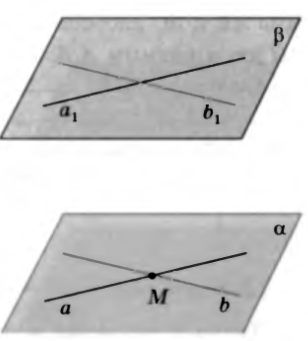Теорема (признак параллельности двух плоскостей). Если две пересекающиеся прямые одной плоскости _____________________________________________ двум прямым другой плоскости, то эти плоскости __________________________.

Дано: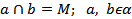

.

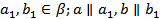Доказать: .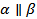

Доказательство. Заметим, что 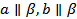по признаку _______

__________________________________________. Теперь допусти, что плоскости α и β не __________________________, а пересекаются по ___________________________________ c. Тогда плоскость α проходит через прямую a, параллельную плоскости _______ , и пересекает плоскость β по прямой c. Следовательно, 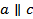. Но плоскость α проходит и ____________ _________________________________________________________________________________ , следовательно, 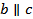. Таким образом, через точку M проходят две прямые ________ , параллельные прямой _____ . Но это невозможно, так как по ______________________________ _______________________________ через точку M ______________________________________ ____________________________ . Значит, наше допущение неверно и 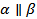. Теорема доказана.

Задачи:

№9. Две стороны треугольника параллельны плоскости α. Докажите, что и третья сторона параллельна плоскости α (задача 52 учебника).

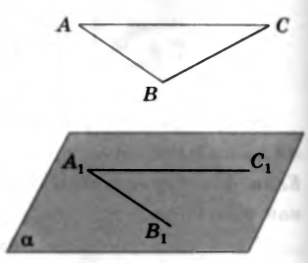Доказательство. Пусть стороны AB и АС треугольника ABC па­раллельны плоскости α. Докажем, что и третья сторона ВС параллель­на плоскости α. Так как АВ ║ α, то, в плоскости α существует некоторая прямая А₁В₁ ║АВ. Аналогично существует пря­мая А₁С₁ плоскости α, параллельная пря­мой AC . Итак, две пересекающиеся пря­мые АВ и АС плоскости ABC параллель­ны двум прямым А₁В₁ и А₁С₁ плоскости α, следовательно, _______________________________________ _______________________________________, эти плоскости ____________________________ , а потому прямая BC __________________________ плоскости α.

№10.

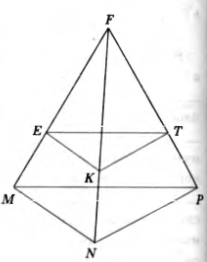Точка F не лежит в плоскости треугольника MNP, точки E, K и T лежат на отрезках FM, FN и FP, причем .

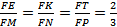а) Докажите, что плоскости EKT и MNP параллельны.

б) Найдите площадь треугольника MNP, если площадь треугольника EKT равна 36 см².

Решение.

а) 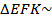_______, так как _______________________________________, поэтому EK║_______ и EK = ___________. Аналогично 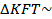________, так как _______________________________________________, поэтому KT ║ _______ и KT = ____________

Итак, пересекающиеся прямые EK и KT плоскости EKT соответственно ____________________ ________________________________________________ плоскости MNP, следовательно, эти плоскости ________________________________________

б) 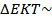___________, так как _______________________________________________________ _________________________________, и коэффициент подобия k равен _______. Поэтому 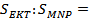_________ =_________, откуда ______________ = ________________

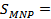Ответ. б) ____________

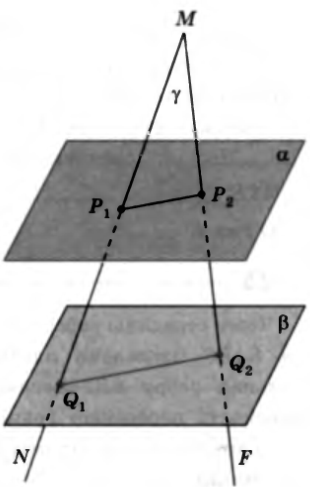№11. На рисунке параллельные плоскости α и β пересечены прямыми MN и MF, P₁, P₂ и Q₁, Q₂ – точки пересечения прямых с плоскостями α и β. Найдите P₁P₂, если MP₁:MQ₁=3:4 и Q₁Q₂ =72 см.

Решение. 1) Пересекающиеся прямые MN и MF задают некоторую ________________ 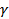. P₁ и P₂ – общие точки плоскостей α и 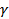, поэтому прямая P₁P₂ - _______________________________, поэтому прямая Q₁Q₂ - __________________

Итак, параллельные плоскости α и β пересечены плоскостью 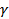, поэтому, согласно _________ ________________________________________________, линии их пересечения ______________ ________________, т.е. P₁P₂║ ______________

2) 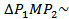__________, так как ______________, следовательно, _______, _____________ = ______________

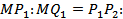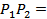Ответ. __________

5.Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости.

Теорема (признак перпендикулярности прямой и плоскости): Если прямая перпендикулярна к двум _________________________ прямым, ________________________ __________________________________________, то она ________________________________ __________________________________

Дано: 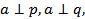прямые p и q лежат в плоскости α и пересекаются в точке O (рис. а).

Доказать: .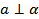

Доказательство. Для доказательства перпендикулярности прямой a и плоскости α надо доказать, что 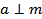, где m - __________________________________________________________

Рассмотрим два случая.

1)Пусть 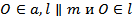, прямая n пересекает прямые p , q и l в точках P , Q , L , OA = OB (рис.б). Так как прямые p и q – серединные __________________________________________ ____________________________, то AP = __________ и AQ = _________, и, следовательно, 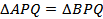по ____________________________________. Поэтому 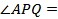____________. Далее 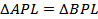по ____________________________________________________________ ________________________________________________________________________, поэтому AL= ______, а это означает, что 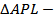___________________________________ и его медиана LO является __________________, т.е. 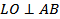или 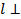____. Так как 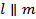и 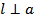, то по лемме 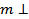_________________________________________________________________________________ ______. Таким образом, прямая a перпендикулярна к любой прямой плоскости α, а это означает, что ____________

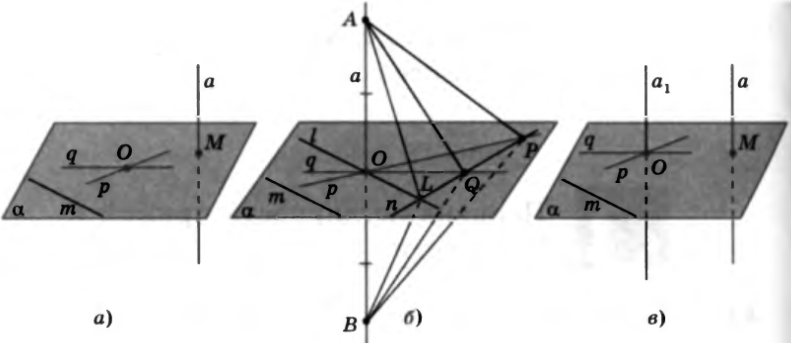
2)Пусть 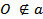(рис.в). Проведем 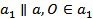. Тогда 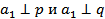по лемме _________ _________________________________________________________________________________ __________________________________________ и, следовательно, 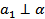согласно _________ _________________________________. Итак, одна из параллельных прямых a и a ₁ перпендикулярна ____________________________, поэтому и вторая прямая _______________ _________________________________________________, т.е. 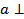_______. Теорема доказана.

№12. Через точку O пересечения диагоналей ромба ABCD проведена прямая OM, перпендикулярная к плоскости ромба, причем OM = 6 см, AC = 16 см, BD = 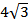см. Найдите:

а) расстояние от точки M до вершин ромба;

б) расстояние от точки M до стороны DC.

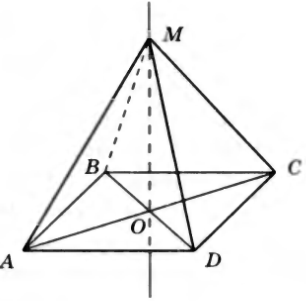Решение. а) Четырехугольник ABCD – ромб, а отрезки AC и BD – его диагонали, пересекающиеся в точке O, поэтому OA = _____, OB = _____. Так как 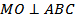, то 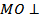____ и 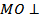_____. В треугольниках AMC и BMD медиана MO является и _______________, поэтому эти треугольники __________________________, т.е. ____________________________________. Из прямоугольного треугольника AOM с катетами 6 см и 8 см имеем: MA = _______. Из прямоугольного треугольника BOM находим: MB = ________________________ см.

Итак, MA = MC = ________, MB = MD = ________

б) В треугольнике DMC проведем 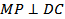и рассмотрим плоскость MOP. Прямая DC перпендикулярна к двум пересекающимся прямым _______ и _______ этой плоскости, следовательно, по ________________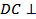_________________________________________________ ________________ _________, а потому перпендикулярна к любой прямой, лежащей в этой плоскости, в частности 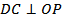. 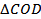прямоугольный, так как ______________________, OP – его высота, поэтому _______________ = _______________

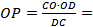Ответ. а) _______________; б) ______________