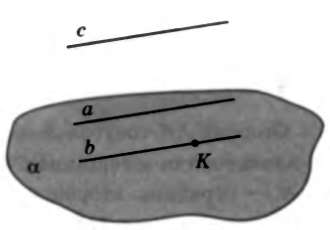
Дано: - точка пересечения прямой a и плоскости .

Дата: 2025-06-15; Просмотры: 1

Оценка:

0.00 из 5.00 — оценок

Скачиваний: 0

Скачать

Доказать: прямая b __________________________

Доказательство: Пусть 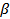– плоскость, в которой лежат параллельные прямые a и b. Так как 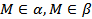, то __________________________ плоскост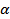и и 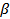пересекаются по некоторой прямой p, проходящей через ___________________. Таким образом, в плоскости 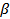прямая p пересекает прямую a в точке ______ , а потому она __________________ и параллельную ей ____________ в некоторой точке N, причем точка 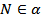, так как _________ . Итак, N – общая точка прямой ____ и плоскости ____. Других общих точек с плоскостью 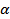прямая b не имеет. Действительно, если предположить, что прямая b ______________________________________ еще одну _______________________, то, согласно _____________________, прямая b будет целиком лежать в __________________ _, а значит, будет общей прямой _________________________ и потому совпадает _____________. Но это невозможно, так как по условию 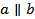, а прямые a и p ____________________________. Лемма доказана.

Теорема (о трех параллельных прямых). Если две прямые параллельны третьей, то они ____________________________.

Дано: .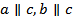

Доказать: _______

Доказательство. Нужно доказать, что прямые a и b:

1) Лежат в одной _____________________.

2) Не _______________________________.

1) Пусть K – какая-нибудь точка на прямой b. Плоскость, проходящую через прямую a и точку K, обозначим буквой 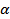. Прямая b лежит в плоскости 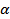, то, согласно лемме ________________________________________________ ___________________________________, прямая c также будет пересекать плоскость 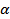. Но 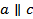, поэтому и прямая a будет _____________________________________________, что невозможно, так как прямая a лежит в _________________________. Итак, прямые a и b лежат в одной плоскости.

2) Прямые a и b не пересекаются, так как в противном случае через точку их пересечения проходили бы ___________________________________, параллельные _______________, что невозможно. Итак, 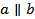. Теорема доказана.

Задачи:

№4. Точка D не лежит в плоскости ABC, точки E , F , G , K – середины отрезков AD , DC , BC и AB.

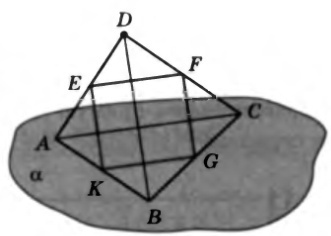а) Докажите, что точки E , F , G , K лежат в одной плоскости.

б) Найдите периметр четырехугольника EFGK, если AC = 18 см, BD = 24 см.

Решение. а) EF – средняя линия треугольника __________, поэтому 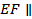_____ и EF = ______; KG – средняя _________________________ и потому _______________.

Следовательно, 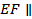_____, т.е. точки E , F , G , K лежат на параллельных прямых, а значит, лежат в одной __________________.

б) Четырехугольник EFGK – параллелограмм, так как ________________________, причем EF = ____________, EK = _______________, а потому ____________________________.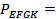

Ответ. б) ____________