Рабочая тетрадь по геометрии
Государственное автономное профессиональное образовательное учреждение Чувашской Республики
«Чебоксарский экономико-технологический колледж»
Министерства образования и молодежной политики Чувашской Республики
Рабочая тетрадь по геометрии
для студентов СПО 1 курса
Разработчик: Чернова Т.В.,
преподаватель математики.
Чебоксары 2021 г.
Рецензия
Данное пособие полностью соответствует примерной учебной и рабочей программам. Способствует самостоятельную работу студентов над освоением учебной дисциплины и формирует практические умения.
Пособие является необходимым дополнением к учебнику Л.С.Атанасяна и др. "Геометрия. 10-11 классы" (издательство "Просвещение").
Основное назначение тетради - обеспечение решения задач студентами на занятиях и дома после ознакомления с новым учебным материалом. Тетрадь окажется полезной и при самостоятельном изучении материала учебника, например, если студент пропустил занятия из-за болезни.
ОГЛАВЛЕНИЕ:
Прямые и плоскости в пространстве.
1. Аксиомы стереометрии
2. Взаимное расположение двух прямых в пространстве. Признак параллельности двух прямых.
3. Признак скрещивающихся прямых.
4. Взаимное расположение двух плоскостей. Признак параллельности двух плоскостей.
5. Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости.
6. Перпендикуляр и наклонная. Теорема о трех перпендикулярах.
7. Угол между прямой и плоскостью.
8. Двугранный угол. Угол между плоскостями. Перпендикулярность двух плоскостей.
Геометрические тела и поверхности.
1.Тело и его поверхность. Многогранники. Призма. Параллелепипед и его свойства.
2. Пирамида. Усеченная пирамида.
3. Правильные многогранники.
4. Поверхность тел вращения. Цилиндр.
5. Конус. Усеченный конус.
6. Шар и сфера.
Прямые и плоскости в пространстве.
1.Аксиомы стереометрии.
А1. Через любые три точки, ________________________________________________________, проходит плоскость, и притом _________________________.
А2. Если две точки прямой лежат в плоскости, то______________________________________ лежат в этой плоскости.
А3. Если две плоскости имеют общую точку, то они имеют _____________________________, на которой лежат ________________________________________ этих плоскостей.
А1 А3
А2
Вопрос. Три точки лежат в каждой из двух различных плоскостей. Можно ли утверждать, что эти точки лежат на одной прямой?
Ответ. Да. Так как каждая точка принадлежит обеим плоскостям, то эти плоскости по аксиоме ______ имеют __________________________________.
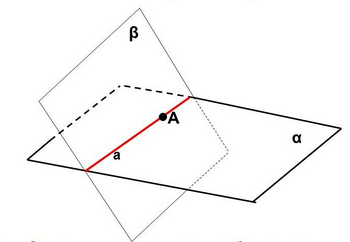
T еорема 1. Через прямую и __________________________________ точку проходит плоскость, и притом ___________________________.
Дано: прямая a , М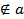 
.
Доказать:
а) через прямую а и точку M проходит плоскость;
б) такая плоскость единственная.
Доказательство.
а) Пусть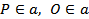 
. Точки _________________ не лежат на одной прямой,
поэтому через эти точки по________________________ проходит некоторая плоскость α. Так как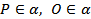 
, то прямая а лежит в плоскости α_______. Итак, плоскость α проходит через точку ______ и _______.
б) Допустим, что через прямую а и точку M проходит еще одна плоскость β. Тогда точки _________ будут лежать и__________________ . Следовательно, по ________________ плоскости α и β __________________ . Таким образом, через точку _______ и ______ проходит_________________ плоскость. Теорема доказана.
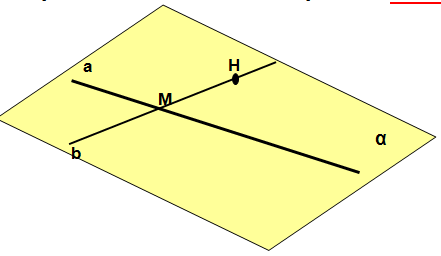Теорема 2. Через две ________________________ прямые проходит плоскость, и притом _____________________ .
Дано: прямые a и b,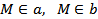 
.
Доказать:
а) через прямые a и b проходит плоскость;
б) такая плоскость единственная.
Доказательство.
а) Пусть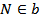 
, причем H и M - ____________________ точки, тогда по ___________________ через прямую a и точку H проходит плоскость 
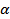. Так как две точки ____ и ____ прямой b лежат в плоскости α, то по _______________ прямая b ___________________. Итак, через прямые a и b проходит ______________________.
б) Допустим, что через прямые a и b проходит еще одна ______________ β. Тогда точка ______ и _______________ лежат в этой плоскости, поэтому, согласно ___________________ , плоскости α и β _______________ . Таким образом, через пересекающиеся прямые ____ и ____ проходит ____________ плоскость. Теорема доказана.
Задачи:
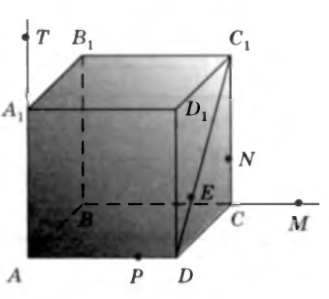№1. На рисунке изображен куб. Назовите:
а) плоскости, в которых лежат прямые NE , MN , TP , PM;
б) точки пересечения прямой MN с плоскостью DCC 1, прямой СЕ с плоскостью ABD , прямой РМ с плоскостью ВСС1;
в) прямые, по которым пересекаются плоскости А B С и В1 C 1 N, AlBlCl и CDE ;
г) точки пересечения прямых АР и ЕС1, DE и B 1 C 1 , AT и A 1 D 1.
Ответ.
а) Прямая NE лежит в плоскости D СС1, прямая MN лежит в плоскости _______, прямая TP лежит в плоскости _______ прямая РМ лежит в плоскости ________.
б) прямая MN пересекает плоскость DCC 1 в точке ______, прямая СЕ пересекает плоскость ABD в точке ______, прямая РМ пересекает плоскость В CC 1 в точке _____.
в) плоскости A ВС и В1 C 1 N 1 пересекаются по прямой _____, плоскости А1В1 C 1 и CDE пересекаются по прямой _____.
г) прямые АР и EC 1 пересекаются в точке ______, прямые DE и В1С1 пересекаются в точке _____, прямые AT и A 1 D 1 пересекаются в точке ______.
№2. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости . Лежат ли две другие вершины параллелограмма в плоскости ? Ответ обоснуйте (задача 9 учебника).
Решение. Пусть смежные вершины В и C и точка О пересечения диагоналей параллелограмма ABCD лежат в плоскости 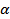. Тогда по аксиоме ______ прямые ______ и ______ лежат в плоскости 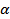, и так как 
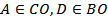, то точки __________________________________________ .
Ответ. ______
№3. Точки M , N , P и Q не лежат в одной плоскости. Могут ли прямые MQ и NP пересекаться?
Ответ. ______. Если бы прямые MQ и NP пересекались, то, согласно ____________, эти прямые лежали бы в _______ плоскости, а поэтому точки _______________ также лежали бы в этой плоскости, что противоречит _____________.
2.Взаимное расположение двух прямых в пространстве. Признак параллельности двух прямых.
Лемма . Если одна из двух __________________________ прямых пересекает данную плоскость, то и _______________________________________ эту плоскость.