З'єднання з повтореннями елементів

Дата: 2025-06-02; Просмотры: 8
Оценка:
0.00 из 5.00 — оценок
Скачиваний: 0

До цих пір розглядали підмножини із скінченних множин, що складаються з різних елементів. Часто на практиці мають місце випадки, коли серед розглянутих елементів є однакові. Тому вводять три типа аналогічних комбінаторних з'єднань, але з елементами, що поможуть повторюватися:

1) перестановки із повтореннями елементів;

2) розміщення із повтореннями елементів;

3) сполучення із повтореннями елементів.

 

Перестановки із повторенням елементів

Дана множина 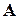, що складається із 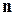елементів, у якій:

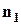– елемент належить першому типу;

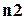– елементів належить другого типу елементів; ;

... ;

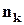– елементів належить 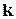-тому типу елементів.

Елементи одного й того ж типу не розрізняються між собою.

Специфікацією множини 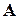називається набір .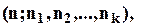

 

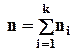Теорема 1

Доведення.

Нехай 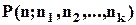– число різних перестановок з повтореннями у множині 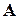. Якщо б всі елементи множини 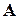були різні, то їх можна було б переставити 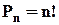способами.

Число 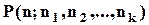менше за 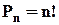у 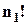разів саме за рахунок перестановок елементів першого типу, у 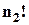– за рахунок елементів 2 типу, та, ..., у 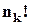– за рахунок елементів 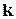-того типу.

 

Слідство

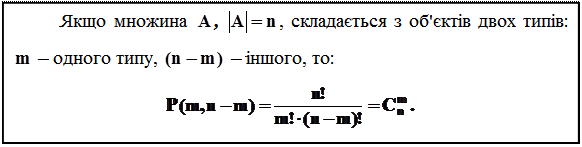
У загальному випадку:

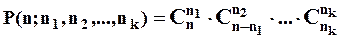
Наприклад.

1) Скількома способами можна переставити букви в слові "каша"?

Розв’язання.

Усього в слові "каша" чотири літери, серед яких дві однакові:

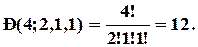
2) Скільки різних чисел можна отримати, переставляючи цифри числа 12341234?

Розв’язання.

У числі 8 цифр: дві – "1", дві – "2", дві – "3", дві – "4". За теоремою 1 маємо:

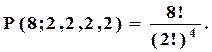
3) Скільки різних перестановок можна утворити з усіх літер слова «Міссісіпі»?

Розв’язання.

Всього в слові 9 букв, з них – 4 літери "і", три літери "с", одна літера "м" та одна літера "п".

.

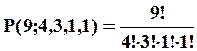4) Тридцять осіб розбиті на 3 групи по 10 чоловік у кожній. Скільки різних складів груп можна скласти?

Розв’язання.

Задача може бути розв’язана двома способами, що випливає із слідства до теореми про перестановки із повтореннями.

Порядок входження людей до груп не має значення. Тоді, спочатку, вибираємо десять чоловік із тридцяти, що увійдуть у першу групу. Це можна зробити 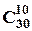способами. Потім, із двадцяти тих, що лишилися, вибираємо десять чоловік для другої групи, й останні десять складуть третю групу. За правилом добутку, маємо:

.

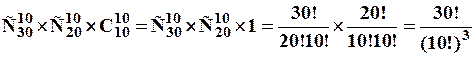Другий спосіб слідкує із безпосереднього застосування логіки теореми про перестановки із повтореннями. Розбиття тридцяти чоловік на три групи можна отримати наступним чином. Взяти усі перестановки тридцяти чоловік: 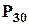та виключити з них перестановки перших десяти: 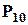, бо вони усі увійдуть у першу групу і перестановки їх між собою враховувати не треба (тобто вони в цьому сенсі вважаються однаковими). Потім аналогічно, виключити перестановки другої десятки та третьої. Тоді, кількість перестановок із повтореннями із специфікацією 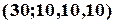дорівнює:

.
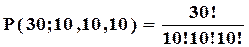