«донецький національний технічний університет»
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»
КАФЕДРА ПРИКЛАДНОЇ МАТЕМАТИКИ І ІНФОРМАТИКИ
МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ
до самостійної роботи та виконання індивідуального завдання за курсом
«ОДМ, частина 1»
Донецьк-2010
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД
«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»
КАФЕДРА ПРИКЛАДНОЇ МАТЕМАТИКИ І ІНФОРМАТИКИ
МЕТОДИЧНІ ВКАЗІВКИ ТА ЗАВДАННЯ
до самостійної роботи та виконання індивідуального завдання за курсом
«ОДМ, частина 1»
для студентів, що навчаються за напрямом підготовки
« Комп’ютерні науки»
Розглянуто на засіданні кафедри
прикладної математики і інформатики
протокол № 11 від 17.05.2010
Затверджено на засіданні
навчально-видавничої ради ДонНТУ
протокол № від . .
Донецьк-2010
УДК 004.021
Методичні вказівки та завдання до самостійної роботи та виконання індивідуального завдання за курсом "ОДМ, частина 1" (для студентів, що навчаються за напрямом підготовки "Комп’ютерні науки ") / Укл.: І.А. Назарова. - Донецьк: ДонНТУ, 2010. - 48с.
Методичні вказівки містять теоретичні матеріали, завдання та приклади розв’язання задач із одного із «Комбінаторного аналізу» - найважливіших розділів курсу “ Основи дискретної математики”.
Укладач: Назарова І.А., к.т.н., доцент
Рецензент Скобцов Ю.О., д.т.н., професор
Вступ
Комбінаторика – розділ математики, що вивчає різні співвідношення між елементами, як правило, скінченних множин.
Основні типи задач
1) Задачі переліку (скільки?):
визначення кількості елементів множини, що володіють заданими властивостями.
2) Задачі генерації або перелічення (які?):
формування списків елементів множини, що володіють заданими властивостями.
3) Задачі комбінаторної оптимізації:
визначення підмножини деякої множини елементів, на якому задана функція приймає мінімальне або максимальне значення.
Правила суми та добутку
Важливу роль при розв’язанні багатьох найбільш простих комбінаторних задач грають правила суми та добутку. Сформулюємо ці правила з точки зору комбінаторики для двомірного випадку.
Правило суми
Якщо об'єкт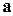 
може бути вибраний 
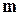способами, а об'єкт 
– 
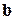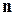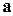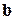іншими способами, то вибір " або " може бути здійснено 
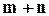способами.
Вибір 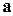і 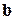– є взаємовиключним: вибір об'єкта 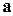виключає вибір об'єкта 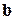; жоден спосіб вибору об'єкта 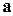не збігається із жодним способом вибору об'єкта .
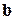Наприклад.
З Києва до Донецька протягом доби відправляється три потяга та один літак. Скільки існує способів виїхати із Києва до Донецька?
Розв’язання.
З Києва до Донецька можна доїхати або потягом, або літаком. Ніякий спосіб їхати потягом не співпадає ні з яким способом, якщо вибрано літак. Якщо летимо, то не їдемо потягом, якщо їдемо потягом, то не летимо, тобто вибір є взаємовиключним. Маємо змогу застосувати правило суми. За правилом суми: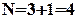 
.
Правило добутку
Якщо об'єкт 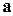може бути вибраний 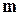способами, і після цього, і незалежно від цього об'єкт 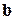може бути вибраний 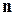способами, то вибір " 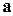та 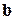" може бути здійснено 
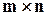способами.
Вибір " 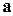та 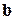" – незалежний: вибір об'єкта 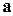не впливає на кількість способів вибору об'єкта .
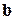Зауваження: правила суми та добутку можуть бути поширені на 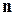- мірний випадок.
Наприклад.
Скільки різних танцюючих пар можна скласти із трьох дівчат та двох юнаків?
Розв’язання.
Для танцюючою пари необхідно вибрати і хлопця, і дівчину. Причому кількість способів вибрати дівчину не залежить від того, якого хлопця вже було обрано. За правилом добутку маємо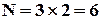 
пар.
Складний вибір об'єктів
Часто у комбінаторних задачах вибір об'єктів здійснюється в кілька етапів, на деяких працює правило суми, на інших – правило добутку. При складному виборі об'єктів важливо забезпечити повний і систематичний перебір усіх можливих випадків, причому жоден із варіантів не повинен бути врахований кілька разів.
Наприклад.
Нехай є три прапори різних кольорів. На флагштоці піднімається сигнал, що складається не менше, ніж із двох прапорів. Скільки різних сигналів можна підняти на флагштоці, якщо порядок прапорів у сигналі враховується?
Розв’язання.
Сигнал можна скласти або із 2-х прапорів, або із 3-х. Позначимо через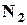 
– кількість способів скласти сигнал із 2-х прапорів, а через 
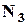– із 3-х відповідно. Одночасне виконання цих двох дій неможливо. Тоді, загальна кількість способів скласти сигнал за правилом суми дорівнює: 
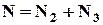. Розрахуємо 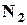. Кількість способів вибрати перший прапор для сигналу, що складається із 2 прапорів, дорівнює 3. Кількість способів вибрати другий прапор для сигналу, що складається із 2 прапорів, дорівнює 2, бо один з 3 прапорів вже був використаний. Треба підняти і перший, і другий прапори, але кількість способів вибрати другий прапор для сигналу не залежить від того, який конкретно прапор був обраний на першому етапі. Тоді, за правилом добутку знаходимо: 
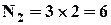. Аналогічно, отримуємо, 
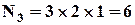, тоді 
.
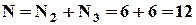Тема 1